The Rate of Reaction, –rA

Identify

– Kind

– Number

– Configuration

The rate of reaction tells us how fast the number of moles of one chemical species are being consumed to form another chemical species. The term chemical species refers to any chemical component or element with a given identity. The identity of a chemical species is determined by the kind, number, and configuration of that species’ atoms. For example, the species para-xylene is made up of a

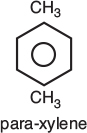
fixed number of specific atoms in a definite molecular arrangement or configuration. The structure shown illustrates the kind, number, and configuration of atoms on a molecular level. Even though two chemical compounds have exactly the same kind and number of atoms of each element, they could still be different species because of different configurations. For example, 2-butene has four carbon atoms and eight hydrogen atoms; however, the atoms in this compound can form two different arrangements.

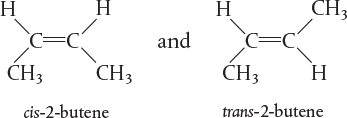
As a consequence of the different configurations, these two isomers display different chemical and physical properties. Therefore, we consider them as two different species, even though each has the same number of atoms of each element.

When has a chemical reaction taken place?

We say that a chemical reaction has taken place when a detectable number of molecules of one or more species have lost their identity and assumed a new form by a change in the kind or number of atoms in the compound and/or by a change in structure or configuration of these atoms. In this classical approach to chemical change, it is assumed that the total mass is neither created nor destroyed when a chemical reaction occurs. The mass referred to is the total collective mass of all the different species in the system. However, when considering the individual species involved in a particular reaction, we do speak of the rate of disappearance of mass of a particular species. The rate of disappearance of a species, say species A, is the number of A molecules that lose their chemical identity per unit time per unit volume through the breaking and subsequent re-forming of chemical bonds during the course of the reaction. In order for a particular species to “appear” in the system, some prescribed fraction of another species must lose its chemical identity.

Definition of Rate of Reaction

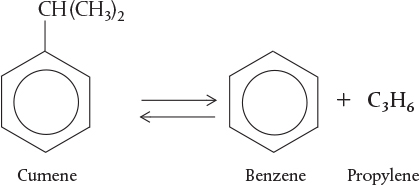
There are three basic ways a species may lose its chemical identity: decomposition, combination, and isomerization. In decomposition, the molecule loses its identity by being broken down into smaller molecules, atoms, or atom fragments. For example, if benzene and propylene are formed from a cumene molecule,

A species can lose its identity by

• Decomposition
• Combination
• Isomerization

the cumene molecule has lost its identity (i.e., disappeared) by breaking its bonds to form these molecules. A second way that a molecule may lose its chemical identity is through combination with another molecule or atom. In the above reaction, the propylene molecule would lose its chemical identity if the reaction were carried out in the reverse direction, so that it combined with benzene to form cumene. The third way a species may lose its chemical identity is through isomerization, such as the reaction

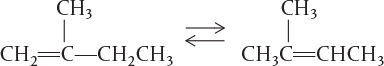
Here, although the molecule neither adds other molecules to itself nor breaks into smaller molecules, it still loses its identity through a change in configuration.

To summarize this point, we say that a given number of molecules (i.e., moles) of a particular chemical species have reacted or disappeared when the molecules have lost their chemical identity.

The rate at which a given chemical reaction proceeds can be expressed in different ways by referring it to different chemical species in the reaction. To illustrate, consider the reaction of chlorobenzene with chloral in the presence of fuming sulfuric acid to produce the banned insecticide DDT (dichlorodiphenyl trichloroethane).

CCl₃CHO + 2C₆H₅Cl → (C₆H₄Cl)₂CHCCl₃ + H₂O

Letting the symbol A represent chloral, B be chlorobenzene, C be DDT, and D be H₂O, we obtain

A + 2B → C + D

What is –r_A?

The rate of reaction, –r_A, is the number of moles of A (e.g., chloral) reacting (disappearing) per unit time per unit volume (mol/dm³·s).

The numerical value of the rate of disappearance of reactant A, –r_A, is a positive number.

Example 1–1 Rates of Disappearance and Formation

Chloral is being consumed at a rate of 10 moles per second per m³ when reacting with chlorobenzene to form DDT and water in the reaction described above. In symbol form, the reaction is written as

A + 2B → C + D

Write the rates of disappearance and formation (i.e., generation; mol/m³·s) for each species in this reaction when the rate of reaction of chloral [A] (–r_A) is 10 mol/m³·s.

NFPA Diamond

DDT See Section 2.7

Solution

(a) Chloral[A]:	Rate of disappearance of A = –rA = 10 mol/m3·sRate of formation of A = rA = –10 mol/m3·s
(b) Chlorobenzene[B]:	For every mole of chloral that disappears, two moles of chlorobenzene [B] also disappear.Rate of disappearance of B = –rB = –2rA = 20 mol/m3·sRate of formation of B = rB = –20 mol/m3·s
(c) DDT[C]:	For every mole of chloral that disappears, one mole of DDT [C] appears. rC = –rARate of disappearance of C = –rC = –10 mol/m3·sRate of formation of C = rC = –rA = –(–10 mol/m3·s) = 10 mol/m3·s
(d) Water[D]:	Same relationship to chloral as the relationship to DDTRate of formation of D = rD = 10 mol/m3·sRate of disappearance of D = –rD = –10 mol/m3·s

–r_A = 10 mol A/m³s^†

r_A = –10 mol A/m³·s

Equation (3-1) page 77

Then

r_B = 2(r_A) = –20 mol B/m³·s

–r_B = 20 mol B/m³·s

r_C = –r_A = 10 mol C/m³·s

r_D = –r_A = 10 mol D/m³·s

A + 2B → C + D

The convention

–r_A = 10 mol A/m³·s

r_A = –10 mol A/m³·s

–r_B = 20 mol B/m³·s

r_B = –20 mol B/m³·s

r_C = 10 mol C/m³·s

Analysis: The purpose of this example is to better understand the convention for the rate of reaction. The symbol r_j is the rate of formation (generation) of species j. If species j is a reactant, the numerical value of r_j will be a negative number. If species j is a product, then r_j will be a positive number. The rate of reaction, –r_A, is the rate of disappearance of reactant A and must be a positive number. A mnemonic relationship to help remember how to obtain relative rates of reaction of A to B, and so on, is given by Equation (3-1) on page 77.

In Equation (3-1) in Chapter 3, we will delineate the prescribed relationship between the rate of formation of one species, r_j (e.g., DDT [C]), and the rate of disappearance of another species, – r_i (e.g., chlorobenzene [B]), in a chemical reaction.

Heterogeneous reactions involve more than one phase. In heterogeneous reaction systems, the rate of reaction is usually expressed in measures other than volume, such as reaction surface area or catalyst weight. For a gas–solid catalytic reaction, the gas molecules must interact with the solid catalyst surface for the reaction to take place, as described in Chapter 10.

What is ?

The dimensions of this heterogeneous reaction rate,  (prime), are the number of moles of A reacting per unit time per unit mass of catalyst (e.g., mol/s·g catalyst).

Definition of r_j

Most of the introductory discussions on chemical reaction engineering in this book focus on homogeneous systems, in which case we simply say that r_j is the rate of formation of species j per unit volume. It is the number of moles of species j generated per unit volume per unit time.

We can say four things about the reaction rate r_j: r_j is

The rate law does not depend on the type of reactor used!!

• The rate of formation of species j (mole/time/volume)
• An algebraic equation
• Independent of the type of reactor (e.g., batch or continuous flow) in which the reaction is carried out
• Solely a function of the properties of the reacting materials and reaction conditions (e.g., species concentration, temperature, pressure, or type of catalyst, if any) at a point in the system