The General Mole Balance Equation (GMBE)

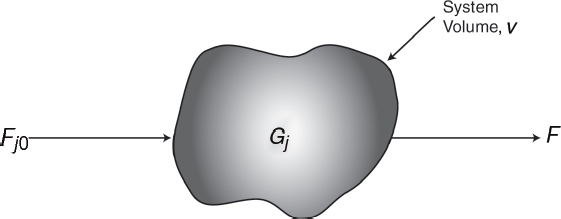
To perform a mole balance on any system, the system boundaries must first be specified. The volume enclosed by these boundaries is referred to as the system volume. We shall perform a mole balance on species j in a system volume, where species j represents the particular chemical species of interest, such as water or NaOH (Figure 1-3).

A mole balance on species j at any instant in time, t, yields the following equation:

Mole balance

Accumulation: In this equation, N_j represents the number of moles of species j in the system at time t and  is the rate of accumulation of species j within the system volume.

Generation: If all the system variables (e.g., temperature, catalytic activity, and concentration of the chemical species) are spatially uniform throughout the system volume, the rate of generation of species j, G_j (moles/time) is just the product of the reaction volume, V, and the rate of formation of species j, r_j.

Now suppose that the rate of formation of species j for the reaction varies with position in the system volume. That is, it has a value r_j1 at location 1, which is surrounded by a small volume, ΔV₁, within which the rate is uniform; similarly, the reaction rate has a value at location 2 and an associated volume, r_j2, and so on (Figure 1-4).

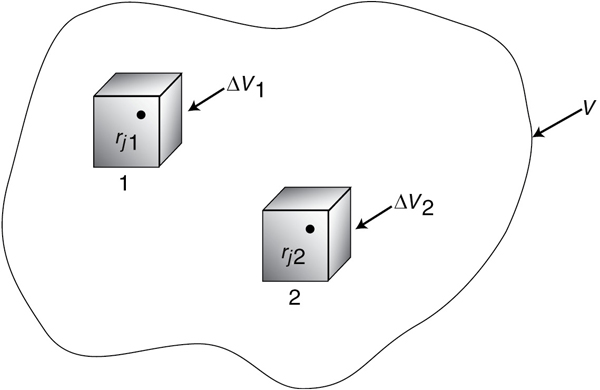
The rate of generation, ΔG_j1, in terms of r_j1 and subvolume ΔV₁, is

ΔG_j1 = r_j1 ΔV₁

Similar expressions can be written for ΔG_j2 and the other system subvolumes, ΔV_i. The total rate of generation within the system volume is the sum of all the rates of generation in each of the subvolumes. If the total system volume is divided into M subvolumes, the total rate of generation is

By taking the appropriate limits (i.e., let M → ∞ and ΔV → 0) and making use of the definition of an integral, we can rewrite the foregoing equation in the form

From this equation, we see that r_j will be an indirect function of position, since the properties of the reacting materials and reaction conditions (e.g., concentration, temperature) can have different values at different locations in the reactor volume.

We now replace G_j in Equation (1-3), that is,

by its integral form to yield a form of the general mole balance equation for any chemical species j that is entering, leaving, reacting, and/or accumulating within any system volume V.

This is a basic equation for chemical reaction engineering.

From this general mole balance equation, we can develop the design equations for the various types of industrial reactors: batch, semibatch, and continuous-flow. Upon evaluation of these equations, we can determine the time (batch), reactor volume or catalyst weight (continuous-flow) necessary to convert a specified amount of the reactants into products.

1.3 Batch Reactors (BRs)

When is a batch reactor used?

A batch reactor is used for small-scale operation, for testing new processes that have not been fully developed, for the manufacture of expensive products, and for processes that are difficult to convert to continuous operations. The reactor can be charged (i.e., filled) through the holes at the top (see Figure 1-5(a)). The batch reactor has the advantage of high conversions that can be obtained by leaving the reactant in the reactor for long periods of time, but it also has the disadvantages of high labor costs per batch, the variability of products from batch to batch, and the difficulty of large-scale production (see Industrial Reactor Photos in Professional Reference Shelf [PRS] (http://www.umich.edu/~elements/6e/01chap/prof-reactors.html) on the CRE Web sites, www.umich.edu/~elements/6e/index.html). Also see http://encyclopedia.che.engin.umich.edu/Pages/Reactors/menu.html.

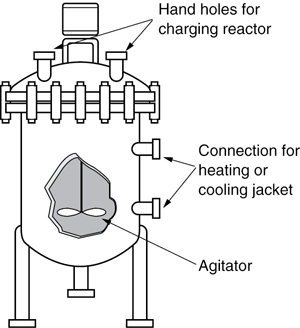
Also see http://encyclopedia.che.engin.umich.edu/Pages/Reactors/Batch/Batch.html.

A batch reactor has neither inflow nor outflow of reactants or products while the reaction is being carried out: F_j0 = F_j = 0. The resulting general mole balance on species j is

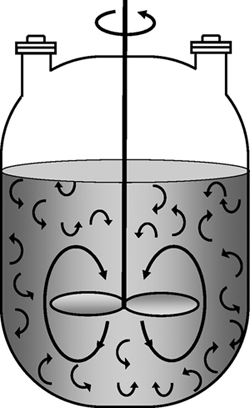
If the reaction mixture is perfectly mixed (Figure 1-5(b)) so that there is no variation in the rate of reaction throughout the reactor volume, we can take r_j out of the integral, integrate, and write the differential form of the mole balance, that is,

Perfect mixing

Let’s consider the isomerization of species A in a batch reactor

As the reaction proceeds, the number of moles of A decreases and the number of moles of B increases, as shown in Figure 1-6.

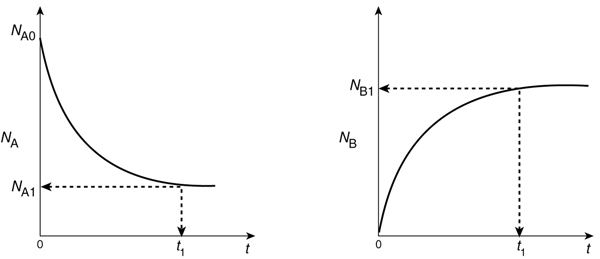
We might ask what time, t₁, is necessary to reduce the initial number of moles from N_A0 to a final desired number N_A1. Applying Equation (1-5) to the isomerization

rearranging,

and integrating with limits that at t = 0, then N_A = N_A0, and at t = t₁, then N_A = N_A1, we obtain

This equation is the integral form of the mole balance on a batch reactor. It gives the time, t₁, necessary to reduce the number of moles from N_A0 to N_A1 and also to form N_B1 moles of B.

1.4 Continuous-Flow Reactors

Continuous-flow reactors are almost always operated at steady state. We will consider three types: the continuous-stirred tank reactor (CSTR), the plug-flow reactor (PFR), and the packed-bed reactor (PBR). Detailed physical descriptions of these reactors can be found in both the Professional Reference Shelf (PRS), (http://www.umich.edu/~elements/6e/01chap/prof.html) of Chapter 1 and in the Visual Encyclopedia of Equipment, http://encyclopedia.che.engin.umich.edu/Pages/Reactors/CSTR/CSTR.html, and on the CRE Web site.