Historically, a large part of thermodynamics was developed before the emergence of atomic and molecular theories of matter. This part has come to be known as classical thermodynamics and makes no reference to molecular concepts. It is based on two basic principles (“laws”) and produces a rigorous mathematical formalism that provides exact relationships between properties and forms the basis for numerical calculations. It is a credit to the ingenuity of the early developers of thermodynamics that they were capable of developing a correct theory without the benefit of molecular concepts to provide them with physical insight and guidance. The limitation is that classical thermodynamics cannot explain why a property has the value it does, nor can it provide a convincing physical explanation for the various mathematical relationships. This missing part is provided by statistical thermodynamics. The distinction between classical and statistical thermodynamics is partly artificial, partly pedagogical. Artificial, because thermodynamics makes physical sense only when we consider the molecular phenomena that produce the observed behaviors. From a pedagogical perspective, however, a proper statistical treatment requires more time to develop, which leaves less time to devote to important engineering applications. It is beyond the scope of this book to provide a bottom-up development of thermodynamics from the molecular level to the macroscopic. Instead, our goal is to develop the knowledge, skills, and confidence to perform thermodynamic calculations in chemical engineering settings. We will use molecular concepts throughout the book to shed light to new concepts but the overall development will remain under the general umbrella of classical thermodynamics. Those who wish to pursue the connection between the microscopic and the macroscopic in more detail, a subject that fascinated some of the greatest scientific minds, including Einstein, should plan to take an upper-level course in statistical mechanics from a chemical engineering, physics, or chemistry program.
The Laws of Classical Thermodynamics
Thermodynamics is built on a small number of axiomatic statements, propositions that we hold to be true on the basis of our experience with the physical world. Statistical and classical thermodynamics make use of different axiomatic statements; the axioms of statistical thermodynamics have their basis on statistical concepts; those of classical thermodynamics are based on behavior that we observe macroscopically. There are two fundamental principles in classical thermodynamics, commonly known as the first and second law.3 The first law expresses the principle that matter has the ability to store energy within. Within the context of classical thermodynamics, this is an axiomatic statement since its physical explanation is inherently molecular. The second law of thermodynamics expresses the principle that all systems, if left undisturbed, will move towards equilibrium –never away from it. This is taken as an axiomatic principle because we cannot prove it without appealing to other axiomatic statements. Nonetheless, contact with the physical world convinces us that this principle has the force a universal physical law.
3. The term law comes to us from the early days of science, a time during which scientists began to recognize mathematical order behind what had seemed up until then to be a complicated physical world that defies prediction. Many of the early scientific findings were known as “laws,” often associated with the name of the scientist who reported them, for example, Dalton’s law, Ohm’s law, Mendel’s law, etc. This practice is no longer followed. For instance, no one refers to Einstein’s famous result, E = mc2, as Einstein’s law.
Other laws of thermodynamics are often mentioned. The “zeroth” law states that, if two systems are in thermal equilibrium with a third system, they are in equilibrium with each other. The third law makes statements about the thermodynamic state at absolute zero temperature. For the purposes of our development, the first and second law are the only two principles needed in order to construct the entire mathematical theory of thermodynamics. Indeed, these are the only two equations that one must memorize in thermodynamics; all else is a matter of definitions and standard mathematical manipulations.
The “How” and the “Why” in Thermodynamics
Engineers must be skilled in the art of how to perform the required calculations, but to build confidence in the use of theoretical tools it is also important to have a sense why our methods work. The “why” in thermodynamics comes from two sources. One is physical: the molecular picture that gives meaning to “invisible” quantities such as heat, temperature, entropy, equilibrium. The other is mathematical and is expressed through exact relationships that connect the various quantities. The typical development of thermodynamics goes like this:
(a) Use physical principles to establish fundamental relationships between key properties. These relationships are obtained by applying the first and second law to the problem at hand.
(b) Use calculus to convert the fundamental relationships from step (a) into useful expressions that can be used to compute the desired quantities.
Physical intuition is needed in order to justify the fundamental relationships in step (a). Once the physical problem is converted into a mathematical one (step [b]), physical intuition is no longer needed and the gear must shift to mastering the “how.” At this point, a good handle of calculus becomes indispensable, in fact, a prerequisite for the successful completion of this material. Especially important is familiarity with functions of multiple variables, partial derivatives and path integrations.
1.3 Definitions
System
The system is the part of the physical world that is the object of a thermodynamic calculation. It may be a fixed amount of material inside a tank, a gas compressor with the associated inlet and outlet streams, or an entire chemical plant. Once the system is defined, anything that lies outside the system boundaries belongs to the surroundings. Together system and surroundings constitute the universe. A system can interact with its surroundings by exchanging mass, heat, and work. It is possible to construct the system in such way that some exchanges are allowed while others are not. If the system can exchange mass with the surroundings it called open, otherwise it is called closed. If it can exchange heat with the surroundings it is called diathermal, otherwise it is called adiabatic. A system that is prevented from exchanging either mass, heat, or work is called isolated. The universe is an isolated system.
A simple system is one that has no internal boundaries and thus allows all of its parts to be in contact with each other with respect to the exchange of mass, work, and heat. An example would be a mole of a substance inside a container. A composite system consists of simple systems separated by boundaries. An example would be a box divided into two parts by a firm wall. The construction of the wall would determine whether the two parts can exchange mass, heat, and work. For example, a permeable wall would allow mass transfer, a diathermal wall would allow heat transfer, and so on.
Classify the systems in Figure 1-5.
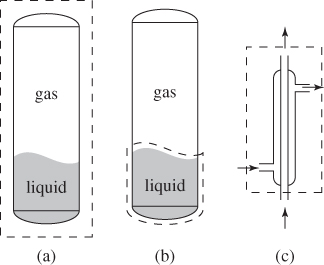
Figure 1-5: Examples of systems (see Example 1.2). The system is indicated by the dashed line. (a) Closed tank that contains some liquid and some gas. (b) The liquid portion in a closed, thermally insulated tank that also contains some gas. (c) Thermally insulated condenser of a laboratory-scale distillation unit.
Solution In (a) we have a tank that contains a liquid and a vapor. This system is inhomogeneous, because it consists of two phases; closed, because it cannot exchange mass with the surroundings; and simple, because it does not contain any internal walls. Although the liquid can exchange mass with the vapor, the exchange is internal to the system. There is no mention of insulation. We may assume, therefore, that the system is diathermal.
In (b) we have the same setup but the system is now defined to be just the liquid portion of the contents. This system is simple, open, and diathermal. Simple, because there are no internal walls; open, because the liquid can exchange mass with the vapor by evaporation or condensation; and diathermal, because it can exchange heat with the vapor. In this case, the insulation around the tank is not sufficient to render the system adiabatic because of the open interface between the liquid and vapor.
In (c) we have a condenser similar to those found in chemistry labs. Usually, hot vapor flows through the center of the condenser while cold water flows on the outside, causing the vapor to condense. This system is open because it allows mass flow through its boundaries. It is composite because of the wall that separates the two fluids. It is adiabatic because it is insulated from the surroundings. Even though heat is transferred between the inner and outer tube, this transfer is internal to the system (it does not cross the system bounds) and does not make the system diathermal.
Comments In the condenser of part (c), we determined the system to be open and adiabatic. Is it not possible for heat to enter through the flow streams, making the system diathermal? Streams carry energy with them and, as we will learn in Chapter 6, this is in the form of enthalpy. It is possible for heat to cross the boundary of the system inside the flow stream through conduction, due to different temperatures between the fluid stream just outside the system and the fluid just inside it. This heat flows slowly and represents a negligible amount compared to the energy carried by the flow. The main mode heat transfer is through the external surface of the system. If this is insulated, the system may be considered adiabatic.
Equilibrium
It is an empirical observation that a simple system left undisturbed, in isolation of its surroundings, must eventually reach an ultimate state that does not change with time. Suppose we take a rigid, insulated cylinder, fill half of it with liquid nitrogen at atmospheric pressure and the other half with hot, pressurized nitrogen, and place a wall between the two parts to keep them separate. Then, we rupture the wall between the two parts and allow the system to evolve without any disturbance from the outside. For some time the system will undergo changes as the two parts mix. During this time, pressure and temperature will vary, and so will the amounts of liquid and vapor. Ultimately, however, the system will reach a state in which no more changes are observed. This is the equilibrium state.
Equilibrium in a simple system requires the fulfillment of three separate conditions:
1. Mechanical equilibrium: demands uniformity of pressure throughout the system and ensures that there is no net work exchanged due to pressure differences.
2. Thermal equilibrium: demands uniformity of temperature and ensures no net transfer of heat between any two points of the system.
3. Chemical equilibrium: demands uniformity of the chemical potential and ensures that there is no net mass transfer from one phase to another, or net conversion of one chemical species into another by chemical reaction.
The chemical potential will be defined in Chapter 7.
Although equilibrium appears to be a static state of no change, at the molecular level it is a dynamic process. When a liquid is in equilibrium with a vapor, there is continuous transfer of molecules between the two phases. On an instantaneous basis the number of molecules in each phase fluctuates; overall, however, the molecular rates to and from each phase are equal so that, on average, there is no net transfer of mass from one phase to the other.
Constrained Equilibrium
If we place two systems into contact with each other via a wall and isolate them from the rest of their surroundings, the overall system is isolated and composite. At equilibrium, each of the two parts is in mechanical, thermal, and chemical equilibrium at its own pressure and temperature. Whether the two parts establish equilibrium with each other will depend on the nature of the wall that separates them. A diathermal wall allows heat transfer and the equilibration of temperature. A movable wall (for example, a piston) allows the equilibration of pressure. A selectively permeable wall allows the chemical equilibration of the species that are allowed to move between the two parts. If a wall allows certain exchanges but not others, equilibrium is established only with respect to those exchanges that are possible. For example, a fixed conducting wall allows equilibration of temperature but not of pressure. If the wall is fixed, adiabatic, and impermeable, there is no exchange of any kind. In this case, each part establishes its own equilibrium independently of the other.
Extensive and Intensive Properties
In thermodynamics we encounter various properties, for example, density, volume, heat capacity, and others that will be defined later. In general, property is any quantity that can be measured in a system at equilibrium. Certain properties depend on the actual amount of matter (size or extent of the system) that is used in the measurement. For example, the volume occupied by a substance, or the kinetic energy of a moving object, are directly proportional to the mass. Such properties will be called extensive. Extensive properties are additive: if an amount of a substance is divided into two parts, one of volume V1 and one of volume V2, the total volume is the sum of the parts, V1 + V2. In general, the total value of an extensive property in a system composed of several parts is the sum of its parts. If a property is independent of the size of the system, it will be called intensive. Some examples are pressure, temperature, density. Intensive properties are independent of the amount of matter and are not additive.
As a result of the proportionality that exists between extensive properties and amount of material, the ratio of an extensive property to the amount of material forms an intensive property. If the amount is expressed as mass (in kg or lb), this ratio will be called a specific property; if the amount is expressed in mole, it will be called a molar property. For example, if the volume of 2 kg of water at 25 °C, 1 bar, is measured to be 2002 cm3, the specific volume is
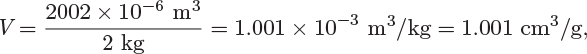
and the molar volume is
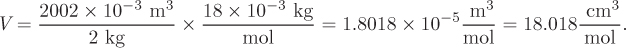
In general for any extensive property F we have a corresponding intensive (specific or molar) property:
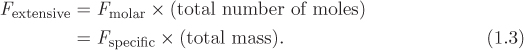
The relationship between specific and molar property is

where Mm is the molar mass (kg/mol).
Note
Nomenclature
We will refer to properties like volume as extensive, with the understanding that they have an intensive variant. The symbol V will be used for the intensive variant, whether molar or specific. The total volume occupied by n mole (or m mass) of material will be written as Vtot, nV, or mV. No separate notation will be used to distinguish molar from specific properties. This distinction will be made clear by the context of the calculation.
State of Pure Component
Experience teaches that if we fix temperature and pressure, all other intensive properties of a pure component (density, heat capacity, dielectric constant, etc.) are fixed. We express this by saying that the state of a pure substance is fully specified by temperature and pressure. For the molar volume V, for example, we write

which reads “V is a function of T and P.” The term state function will be used as a synonym for “thermodynamic property.” If eq. (1.5) is solved for temperature, we obtain an equation of the form

which reads “T is a function of P and V.” It is possible then to define the state using pressure and molar volume as the defining variables, since knowing pressure and volume allows us to calculate temperature. Because all properties are related to pressure and temperature, the state may be defined by any combination of two intensive variables, not necessarily T and P. Temperature and pressure are the preferred choice, as both variables are easy to measure and control in the laboratory and in an industrial setting. Nonetheless, we will occasionally consider different sets of variables, if this proves convenient.
Note
Fixing the State
If two intensive properties are known, the state of single-phase pure fluid is fixed, i.e., all other intensive properties have fixed values and can be obtained either from tables or by calculation.
State of Multicomponent Mixture
The state of a multicomponent mixture requires the specification of composition in addition to temperature and pressure. Mixtures will be introduced in Chapter 8. Until then the focus will be on single components.
Process and Path
The thermodynamic plane of pure substance is represented by two axes, T and P. A point on this plane represents a state, its coordinates corresponding to the temperature and pressure of the system. The typical problem in thermodynamics involves a system undergoing a change of state: a fixed amount of material at temperature TA and pressure PA is subjected to heating/cooling, compression/expansion, or other treatments to final state (TC, PC). A change of state is called a process. On the thermodynamic plane, a process is depicted by a path, namely, a line of successive states that connect the initial and final state (see Figure 1-6). Conversely, any line on this plane represents a process that can be realized experimentally. Two processes that are represented by simple paths on the TP plane are the constant-pressure (or isobaric) process, and the constant-temperature (or isothermal) process. The constant-pressure process is a straight line drawn at constant pressure (path AB in Figure 1-6); the constant-temperature process is drawn at constant temperature (path BC). Any two points on the TP plane can be connected using a sequence of isothermal and isobaric paths.
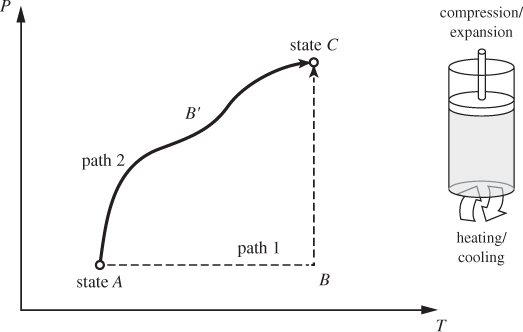
Figure 1-6: Illustration of two different paths (ABC, AB′C) between the same initial (A) and final (C) states. Paths can be visualized as processes (heating/cooling, compression/expansion) that take place inside a cylinder fitted with a piston.
Processes such as the constant-pressure, constant-temperature, and constant-volume process are called elementary. These are represented by simple paths during which one state variable (pressure, temperature, volume) is held constant. They are also simple to conduct experimentally. One way to do this is using a cylinder fitted with a piston. By fitting the piston with enough weights we can exert any pressure on the contents of the cylinder, and by making the piston movable we allow changes of volume due to heating/cooling to take place while keeping the pressure inside the cylinder constant. To conduct an isothermal process we employ the notion of a heat bath, or heat reservoir. Normally, when a hot system is used to supply heat to a colder one, its temperature drops as a result of the transfer of heat. If we imagine the size of the hot system to approach infinity, any finite transfer of heat to (or from) another system represents an infinitesimal change for the large system and does not change its temperature by any appreciable amount. The ambient air is a practical example of a heat bath with respect to small exchanges of heat. A campfire, for example, though locally hot, has negligible effect on the temperature of the air above the campsite. The rising sun, on the other hand, changes the air temperature appreciably. Therefore, the notion of an “infinite” bath must be understood as relative to the amount of heat that is exchanged. A constant-temperature process may be conducted by placing the system into contact with a heat bath. Additionally, the process must be conducted in small steps to allow for continuous thermal equilibration. The constant-volume process requires that the volume occupied by the system remain constant. This can be easily accomplished by confining an amount of substance in a rigid vessel that is completely filled. Finally, the adiabatic process may be conducted by placing thermal insulation around the system to prevent the exchange of heat.
We will employ cylinder-and-piston arrangement primarily as a mental device that allows us to visualize the mathematical abstraction of a path as a physical process that we could conduct in the laboratory.
Quasi-Static Process
At equilibrium, pressure and temperature are uniform throughout the system. This ensures a well-defined state in which, the system is characterized by a single temperature and single pressure, and represented by a single point on the PT plane. If we subject the system to a process, for example, heating by placing it into contact with a hot source, the system will be temporarily moved away from equilibrium and will develop a temperature gradient that induces the necessary transfer of heat. If the process involves compression or expansion, a pressure gradient develops that moves the system and its boundaries in the desired direction. During a process the system is not in equilibrium and the presence of gradients implies that its state cannot be characterized by a single temperature and pressure. This introduces an inconsistency in our depiction of processes as paths on the TP plane, since points on this plane represent equilibrium states of well-defined pressure and temperature. We resolve this difficulty by requiring the process to take place in a special way, such that the displacement of the system from equilibrium is infinitesimally small. A process conducted in such manner is called quasi static. Suppose we want to increase the temperature of the system from T1 to T2. Rather than contacting the system with a bath at temperature T2, we use a bath at temperature T1 + δT, where δT is a small number, and let the system equilibrate with the bath. This ensures that the temperature of the system is nearly uniform (Fig. 1-7). Once the system is equilibrated to temperature T1 + δT, we place it into thermal contact with another bath at temperature T1 + 2δT, and repeat the process until the final desired temperature is reached. Changes in pressure are conducted in the same manner. In general, in a quasi-static process we apply small changes at a time and wait between changes for the system to equilibrate. The name derives from the Latin quasi (“almost”) and implies that the process occurs as if the system remained at a stationary equilibrium state.
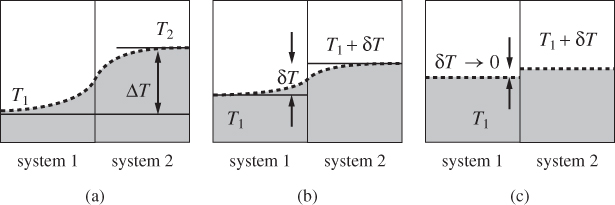
Figure 1-7: (a) Typical temperature gradient in heat transfer. (b) Heat transfer under small temperature difference. (c) Quasi-static idealization: temperatures in each system are nearly uniform and almost equal to each other.
Leave a Reply