The first step to knowledge is to know that we are ignorant.
—Socrates (470–399 B.C.)
The Wide, Wild World of Chemical Reaction Engineering
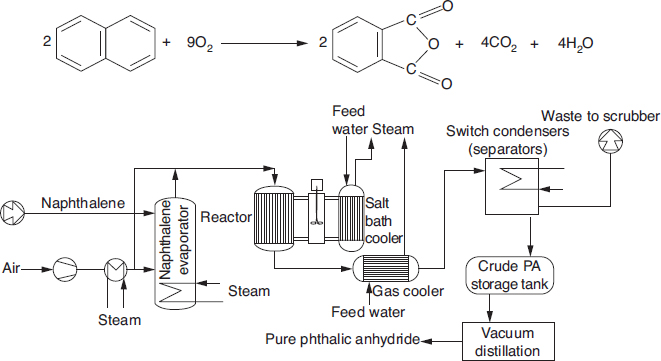
Chemical kinetics is the study of chemical reaction rates and reaction mechanisms. The study of chemical reaction engineering (CRE) combines the study of chemical kinetics with the reactors in which the reactions occur. Chemical kinetics and reactor design are at the heart of producing almost all industrial chemicals, such as the manufacture of phthalic anhydride shown in Figure 1-1. It is primarily a knowledge of chemical kinetics and reactor design that distinguishes the chemical engineer from other engineers. The selection of a reaction system that operates in the safest and most efficient manner can be the key to the economic success or failure of a chemical plant. For example, if a reaction system produces a large amount of undesirable product, subsequent purification and separation of the desired product could make the entire process economically unfeasible.
How is a chemical engineer different from other engineers?
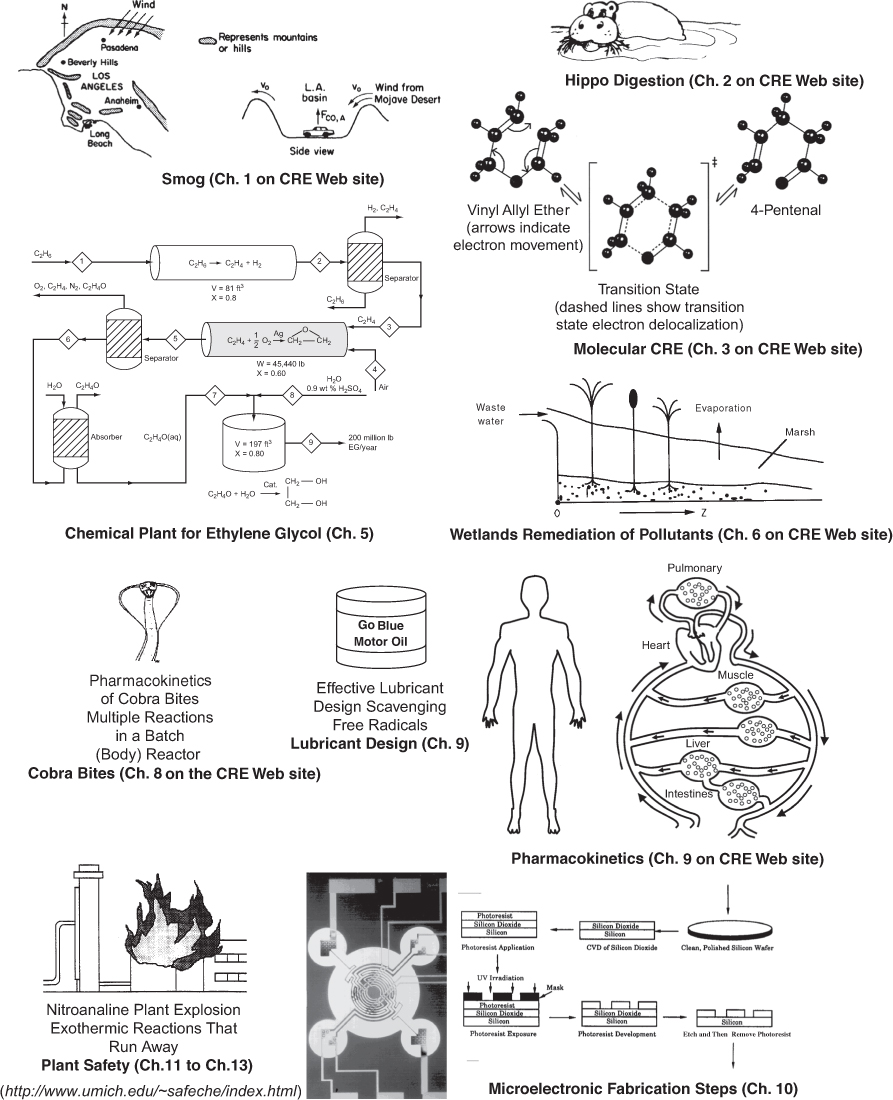
The chemical reaction engineering (CRE) principles learned here can also be applied in many areas, such as waste water treatment, microelectronics, nanoparticles fabrication, and pharmacokinetics of living systems, in addition to the more traditional areas of the manufacture of chemicals and pharmaceuticals. Some of the examples that illustrate the wide application of CRE principles in this book are shown in Figure 1-2. These examples, which can be found either in the text or as Web modules (www.umich.edu/~elements/6e/index.html), include modeling smog in the Los Angeles (L.A.) basin (Chapter 1 Web module), the digestive system of a hippopotamus (Chapter 2 Web module), molecular CRE (Chapter 3 Web module), use of wetlands to degrade toxic chemicals (Chapter 6 on the CRE Web site); pharmacokinetics of cobra bites (Chapter 8 Web module); free-radical scavengers used in the design of motor oils (Chapter 9); enzyme kinetics (Chapter 9) and drug delivery pharmacokinetics (Chapter 9 on the CRE Web site). Also shown in Figure 1-2 are the manufacture of ethylene glycol (antifreeze), where three of the most common types of industrial reactors are used (Chapters 5 and 6). Other examples shown are heat effects, runaway reactions, and plant safety (Chapters 11–13); and increasing the octane number of gasoline and the manufacture of computer chips (Chapter 10).
Overview. This chapter develops the first building block of chemical reaction engineering, mole balances, which will be used continually throughout the text. After completing this chapter, you will be able to:
- Describe and define the rate of reaction
- Derive the general mole balance equation
- Apply the general mole balance equation to the four most common types of industrial reactors
Before entering into discussions of the conditions that affect chemical reaction rates mechanisms and reactor design, it is necessary to account for the various chemical species entering, leaving, reacting, and accumulating in a system. This accounting process is achieved through overall mole balances on individual species in the reacting system. In this chapter, we develop a general mole balance that can be applied to any species (usually a chemical compound) entering, leaving, reacting, and accumulating within the reaction system volume. After defining the rate of reaction, –rA, we show how the general mole balance equation (GMBE) may be used to develop a preliminary form of the design equations of the most common industrial reactors (http://encyclopedia.che.engin.umich.edu/Pages/Reactors/menu.html).
- Batch Reactor (BR)
- Continuous-Stirred Tank Reactor (CSTR)
- Plug-Flow Reactor (PFR)
- Packed-Bed Reactor (PBR)
In developing these equations, the assumptions pertaining to the modeling of each type of reactor are delineated. Finally, a brief summary and series of short review questions and problems are given at the end of the chapter.
1.1 The Rate of Reaction, –rA
Identify
– Kind
– Number
– Configuration
The rate of reaction tells us how fast the number of moles of one chemical species are being consumed to form another chemical species. The term chemical species refers to any chemical component or element with a given identity. The identity of a chemical species is determined by the kind, number, and configuration of that species’ atoms. For example, the species para-xylene is made up of a
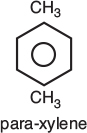
fixed number of specific atoms in a definite molecular arrangement or configuration. The structure shown illustrates the kind, number, and configuration of atoms on a molecular level. Even though two chemical compounds have exactly the same kind and number of atoms of each element, they could still be different species because of different configurations. For example, 2-butene has four carbon atoms and eight hydrogen atoms; however, the atoms in this compound can form two different arrangements.
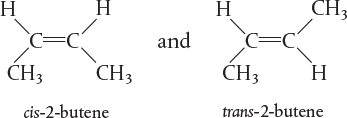
As a consequence of the different configurations, these two isomers display different chemical and physical properties. Therefore, we consider them as two different species, even though each has the same number of atoms of each element.
When has a chemical reaction taken place?
We say that a chemical reaction has taken place when a detectable number of molecules of one or more species have lost their identity and assumed a new form by a change in the kind or number of atoms in the compound and/or by a change in structure or configuration of these atoms. In this classical approach to chemical change, it is assumed that the total mass is neither created nor destroyed when a chemical reaction occurs. The mass referred to is the total collective mass of all the different species in the system. However, when considering the individual species involved in a particular reaction, we do speak of the rate of disappearance of mass of a particular species. The rate of disappearance of a species, say species A, is the number of A molecules that lose their chemical identity per unit time per unit volume through the breaking and subsequent re-forming of chemical bonds during the course of the reaction. In order for a particular species to “appear” in the system, some prescribed fraction of another species must lose its chemical identity.
Definition of Rate of Reaction
There are three basic ways a species may lose its chemical identity: decomposition, combination, and isomerization. In decomposition, the molecule loses its identity by being broken down into smaller molecules, atoms, or atom fragments. For example, if benzene and propylene are formed from a cumene molecule,
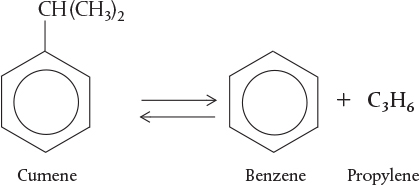
A species can lose its identity by
- Decomposition
- Combination
- Isomerization
the cumene molecule has lost its identity (i.e., disappeared) by breaking its bonds to form these molecules. A second way that a molecule may lose its chemical identity is through combination with another molecule or atom. In the above reaction, the propylene molecule would lose its chemical identity if the reaction were carried out in the reverse direction, so that it combined with benzene to form cumene. The third way a species may lose its chemical identity is through isomerization, such as the reaction
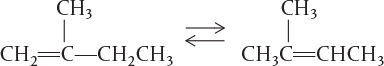
Here, although the molecule neither adds other molecules to itself nor breaks into smaller molecules, it still loses its identity through a change in configuration.
To summarize this point, we say that a given number of molecules (i.e., moles) of a particular chemical species have reacted or disappeared when the molecules have lost their chemical identity.
The rate at which a given chemical reaction proceeds can be expressed in different ways by referring it to different chemical species in the reaction. To illustrate, consider the reaction of chlorobenzene with chloral in the presence of fuming sulfuric acid to produce the banned insecticide DDT (dichlorodiphenyl trichloroethane).
CCl3CHO + 2C6H5Cl → (C6H4Cl)2CHCCl3 + H2O
Letting the symbol A represent chloral, B be chlorobenzene, C be DDT, and D be H2O, we obtain
A + 2B → C + D
What is –rA?
The rate of reaction, –rA, is the number of moles of A (e.g., chloral) reacting (disappearing) per unit time per unit volume (mol/dm3·s).
The numerical value of the rate of disappearance of reactant A, –rA, is a positive number.
Example 1–1 Rates of Disappearance and Formation
Chloral is being consumed at a rate of 10 moles per second per m3 when reacting with chlorobenzene to form DDT and water in the reaction described above. In symbol form, the reaction is written as
A + 2B → C + D
Write the rates of disappearance and formation (i.e., generation; mol/m3·s) for each species in this reaction when the rate of reaction of chloral [A] (–rA) is 10 mol/m3·s.
NFPA Diamond
DDT See Section 2.7
Solution
| (a) Chloral[A]: | Rate of disappearance of A = –rA = 10 mol/m3·sRate of formation of A = rA = –10 mol/m3·s |
| (b) Chlorobenzene[B]: | For every mole of chloral that disappears, two moles of chlorobenzene [B] also disappear.Rate of disappearance of B = –rB = –2rA = 20 mol/m3·sRate of formation of B = rB = –20 mol/m3·s |
| (c) DDT[C]: | For every mole of chloral that disappears, one mole of DDT [C] appears. rC = –rARate of disappearance of C = –rC = –10 mol/m3·sRate of formation of C = rC = –rA = –(–10 mol/m3·s) = 10 mol/m3·s |
| (d) Water[D]: | Same relationship to chloral as the relationship to DDTRate of formation of D = rD = 10 mol/m3·sRate of disappearance of D = –rD = –10 mol/m3·s |
–rA = 10 mol A/m3s†
rA = –10 mol A/m3·s
Then
rB = 2(rA) = –20 mol B/m3·s
–rB = 20 mol B/m3·s
rC = –rA = 10 mol C/m3·s
rD = –rA = 10 mol D/m3·s
†Tutorial Video: https://www.youtube.com/watch?v=6mAqX31RRJU
A + 2B → C + D
The convention
–rA = 10 mol A/m3·s
rA = –10 mol A/m3·s
–rB = 20 mol B/m3·s
rB = –20 mol B/m3·s
rC = 10 mol C/m3·s
Analysis: The purpose of this example is to better understand the convention for the rate of reaction. The symbol rj is the rate of formation (generation) of species j. If species j is a reactant, the numerical value of rj will be a negative number. If species j is a product, then rj will be a positive number. The rate of reaction, –rA, is the rate of disappearance of reactant A and must be a positive number. A mnemonic relationship to help remember how to obtain relative rates of reaction of A to B, and so on, is given by Equation (3-1) on page 77.
In Equation (3-1) in Chapter 3, we will delineate the prescribed relationship between the rate of formation of one species, rj (e.g., DDT [C]), and the rate of disappearance of another species, – ri (e.g., chlorobenzene [B]), in a chemical reaction.
Leave a Reply