A classical mechanical system is characterized by a set of mechanical state variables: velocity, elevation in a gravitational field, electrical charges, and so forth. If these variables are given and the external fields are known, the system is fully specified and its behavior at any instant of time, past or future, can be calculated. Thermodynamic systems are characterized by an additional state variable: temperature. Unlike mechanical variables, which describe external interactions, temperature characterizes the internal state of macroscopic matter. Temperature is a measure of the energy stored inside matter in various forms, which we collectively call internal energy. Temperature gives rise to another type of energy exchange that is not encountered among purely mechanical systems, heat: when two systems, each at its own temperature, are put into thermal contact, energy in the form of heat flows from the higher temperature to the lower temperature. For the complete energy balance, heat and internal energy must both be accounted for.
The incorporation of heat effects into the energy balance constitutes one of the fundamental principles of thermodynamics known as the first law. This chapter is devoted to the mathematical formulation of the first law and in the definition of two thermodynamic properties, internal energy and enthalpy, both of which are important in the calculation of energy balances.
Instructional Objectives In this chapter we will formulate the mathematical statement of the first law for a closed system and will learn how to:
1. Do energy balances in closed systems.
2. Distinguish between path and state functions.
3. Use the steam tables to calculate internal energy and enthalpy.
4. Use heat capacities to calculate changes in internal energy and enthalpy.
5. Apply the energy balance to systems undergoing vaporization or condensation.
6. Perform calculations of internal energy and enthalpy in the ideal-gas state.
3.1 Energy and Mechanical Work
Heat, work and energy are measured in the same units but they represent different physical entities. We begin with work and energy, which are familiar concepts from mechanics. Energy is the ability of a system to produce work, namely, ability to cause the displacement of a force. Consider an object with mass m resting on the floor (Figure 3-1). To lift it to the top of the table at height Δz above ground, we must supply an amount of work equal to W = mgΔz. When the mass is resting on the desk, its potential energy has increased by ΔEp = mgΔz, and the work done to lift the object is now part of the energy of the body and is stored as potential energy. The energy added to the system will stay with it for as long it remains at rest on the table. This could be hours, days, or millennia: potential energy is preserved for as long as the state of the system, in this case elevation, is preserved. The more general conclusion to be drawn from this analysis is that energy is a property of the state and as such, a storable quantity. We can recover it by letting the mass drop to the floor and use its kinetic energy to, say, catapult a small projectile into the air, or to load a spring, or to push a nail into the floor.
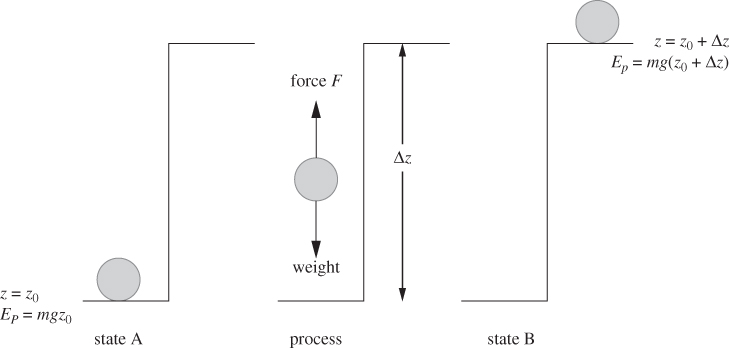
Figure 3-1: Potential energy and mechanical work. From state A to state B the potential energy increases by the amount of work needed to lift the weight. This work must be supplied from the surroundings, that is, from a force external to the system.
Let us focus on work now. Work takes place when a force is displaced. If we lift the weight ourselves, this work is supplied through the action of our muscle. Once the object is placed on the table, there is no more displacement, thus no more work: work is exchanged during a process. It characterizes, not the state of the system, but the transition of the system between states (from the floor to the top of the desk). In thermodynamic terms, the picture illustrated in Figure 3-1 would be described as follows: A system initially in equilibrium state A undergoes a process that brings it to final state B; during this process the system exchanges work with the surroundings so that the energy change of the system is equal to the amount of work exchanged:

This equation reads, “as a result of the process, the energy of the system in state B has increased relative to A by the amount of work added.” Also notice that work represents energy that passes from one system into another. In this example, our muscle (chemical energy) transfers work to the lifted object, where it is converted into potential energy. As a transfer quantity, work is characterized by a direction, “from” (the muscle) “to” (the system). Finally, when work passes into a new system, it is converted into some form of energy (in our example, potential), which now is property of the state. Let us summarize:
• Energy is storable; it remains in the system for as long as the state of the system is preserved. It is a state function.
• Work is energy in transit: it appears when energy is passed from one system into another.
• Work is not a storable quantity as such.1 Work that enters a system must be stored in some form of energy.
1. By this we mean that it is incorrect to say that a system “stores work”; the proper statement is, the system “stores energy.”
• Work is associated with a direction “from” one system in which it originates, “to” another, where it is transferred to.
To indicate the direction of the transfer we adopt a sign convention:
Sign convention for work: Work is positive if it enters the system, negative if it exits.
When the surroundings do the work, the work is positive because it is absorbed by the system. When the work is negative, it is done by the system and absorbed by the surroundings. Clearly, the sign depends on the definition of the system since work that enters one system (the “system”) exits the other (the “surroundings”) and vice versa. To avoid ambiguity, the definition of the system must be made clear when we report positive or negative values of work.
Note
Forms of Energy
As a matter of classification, energy comes in two basic forms, kinetic, and potential. Kinetic is energy stored in the motion of a moving object. Potential energy is a more general category and encompasses several forms that arise from various conservative forces, such as gravitational fields, electric charges, spring forces, and others. All forms of potential energy have the common characteristic that they are described by a potential function Φ(x, y, z) that depends on the space coordinates, x, y, z, and has the property that the force in a given direction is equal to the negative derivative of the potential with respect to the corresponding coordinate:
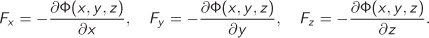
As an example, in the gravitational potential Φ(x, y, z) = mgz, the force (weight) in the z direction is
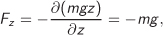
with the negative sign indicating that the weight points downwards. The forces in the x and y direction are both zero. The intermolecular potential introduced in Section 1.1 is another example of potential energy.
3.2 Shaft Work and PV Work
A direct method by which to exchange work with a fluid is through the use of a mechanical device. When wind blows through a turbine, it produces work that is manifested in the rotational motion of the turbine. A centrifugal pump imparts work to a fluid through the rotation of an impeller. This type of work is called shaft work. It will generally be recognizable through the presence of a rotating or reciprocating shaft that absorbs work from a fluid or imparts work to it.
Another more subtle form of work is associated with movement of the system boundaries. Thermodynamic systems make mechanical contact through the pressure that is exerted on the boundaries that separate them. At equilibrium, this pressure is equal on both sides of the boundary. If a pressure imbalance arises between the system and its surroundings, the boundaries of the system must move in response to the mechanical force. Such imbalance may arise from the application of a mechanical force that acts to compress or expand the system, or through the application of heat, which causes the volume to expand or contract. The movement of boundaries involves the exchange of work, which we call PV work.
To obtain an equation for the PV work, consider the compression of a gas in a cylinder fitted with a piston whose area is a (Fig. 3-2b). Compression is done through the application of an external pressure Pex, which produces a force on the piston, F = Pexa, and causes the piston to move by dx. The amount of work associated with this process is equal to the force on the piston, Pexa, multiplied by the displacement dx. Noting that the product adx is equal to the change of volume, −dV, the amount of work is
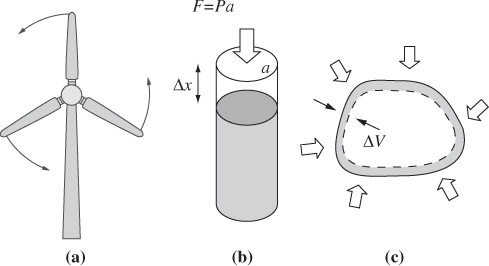
Figure 3-2: Examples of work: (a) shaft work (wind turbine); (b) PV work for compression/ expansion of a gas in a cylinder; (c) PV work associated with volume changes.
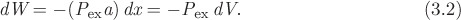
The negative sign is consistent with the convention adopted for work: in compression, dV is negative and the work is positive (it is added to the system); in expansion, dV is positive and the work is negative (work is transferred from the system to the surroundings).
Equation (3.2) gives the work in terms of the external pressure that causes the change. It is more convenient, however, to relate the work to the pressure of the system. For compression, the external pressure must be higher than the pressure of the system, P, which means, Pex = P + δP, where δP is a positive increment; for expansion, δP is negative. If the process is conducted in a quasi-static manner, then δP → 0 and Pex → P. Such process is called mechanically reversible and in this case the PV work is
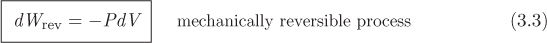
This is the differential amount of work along a small step of a process that causes a volume change. The total amount of work involved in taking the system from an initial state A to final state B along a reversible path is obtained by integration:
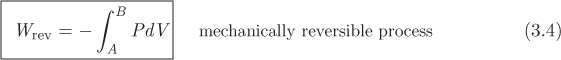
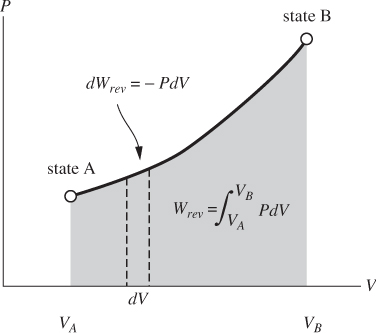
Figure 3-3: Graphical interpretation of reversible PV work.
This result is general and not limited to gases, nor to objects of cylindrical shape. It applies to any system, gas, liquid, or solid, whose volume changes by compression or expansion, under or against the opposing pressure of the surroundings. The only requirement is that the process must be mechanically reversible.
Reversible PV work has a simple graphical interpretation on the PV graph: it is equal in absolute value to the area under the path of the process when this is plotted on the PV graph (Figure 3-3). The sign indicates whether the work is added to or removed from the system. For a path that moves in the direction of increasing V, the area is by convention positive and the work is negative: the system expands and does work against the surroundings. For a process that moves in the direction of decreasing V (compression), the area is negative and the work is positive.
An important conclusion is that PV work depends on the entire path that connects the two states. Different paths between the same two states generally correspond to different areas, and thus different amounts of work. Therefore, the PV work is a path function whose value depends not only on the initial and final states, but on the entire path. This is in contrast to thermodynamic properties (state functions) whose value depends on the state alone.
Example 3.1: PV Work in Expansion
A cylinder fitted with a piston contains 1 liter of gas. The piston has a 1-in diameter and weighs 5 kg. How much work is needed to expand the gas reversibly to twice its volume against the pressure of the atmosphere (1.013 bar)?
Solution The gas expands against the combined pressure of the piston and the atmosphere. The weight of the piston is Mg = (5 kg)(9.81 m/s2)= 49.05 N and the area of the piston is πD2/4 = π(2.54 × 10−2 m)2 = 5.067 × 10−4 m2. The pressure exerted by the piston is
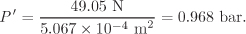
The total pressure in the cylinder is
P = P′ + P0 = 0.968 bar + 1.013 bar = 1.981 bar.
The expansion is to take place against an external pressure of 1.981 bar, which remains constant during the process. If the volume doubles, the change in volume is 1 L = 1000 cm3 = 10−3 m3. The corresponding amount of work is
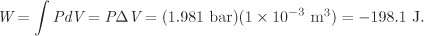
The negative sign indicates that this work is done by the system on to the surroundings.
Example 3.2: PV Work Using the Soave-Redlich-Kwong Equation of State
Ethylene is compressed reversibly in a closed system. The compression is conducted isothermally at 350 K, from initial pressure 20 bar to final pressure 55 bar. Calculate the work using the SRK equation of state.
Solution First, we write the SRK equation in the form,
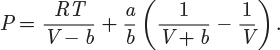
To obtain the work, this pressure must be integrated at constant temperature as a function of V:
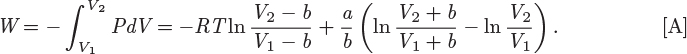
Numerical substitutions The critical parameters of ethylene and the acentric factor are:
Tc = 282.35 K, Pc = 50.418 bar, ω = 0.0866.
Using these values, the constants a and b are:
a = 0.404344 J m3/mol2, b = 4.03395 × 10−5 m3/mol.
The volume V1 must be obtained by solving the SRK equation. As in Example 2.11, we solve for the compressibility factor first. At the initial state (20 bar, 350 K), the equation for Z is
Z3 − Z2 + 0.0670103Z − 0.00264794 = 0.
This equation has one real root, Z = 0.931084, from which we obtain the molar volume of the initial state:
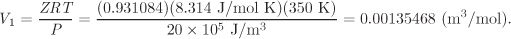
In the final state, the equation for the compressibility factor is
Z3 − Z2 + 0.180579Z − 0.020025 = 0.
This equation has one real root, Z = 0.806979, and the corresponding molar volume is
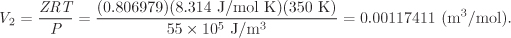
Finally, by numerical substitution into eq. [A], the isothermal work is
W = 385.6 J/mol.
The work is positive, as it should be, since volume decreases.
Example 3.3: Isothermal Compression of Steam
Steam undergoes reversible isothermal compression at 350 °C, from initial pressure 20 bar to 40 bar. Calculate the amount of work.
Solution This problem is very similar to the previous one (see Example 3.2). Here, however, the pressure-volume relationship is given in tabular form and the integration of the PV work must be done numerically. First, we collect values of the specific volume V at 350 °C at various pressures between the final and initial state:
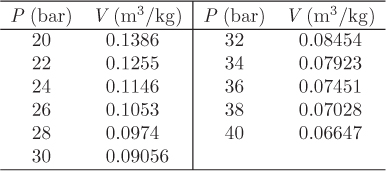
One way to perform the integration is using the trapezoidal rule within each pressure interval. An alternative method, which is generally more accurate, is to fit an equation to the data and perform the integration analytically using the fitted equation. We will illustrate the use of both methods.
Trapezoidal rule: In this method, the integral of n tabulated values {xi, fi} of a function f(x) is given by the following approximation:
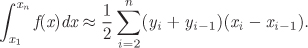
Using xi = Vi, yi = Pi, we construct the following table:

From the sum of the last column we find,
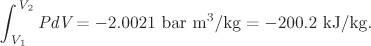
The work is given by the negative of the above integral:
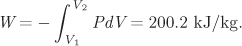
Fitting the data: The data are fitted to a quadratic polynomial in V,
P = a0 + a1 V + a2V2
with coefficients
a0 = 81.4217, a1 = −801.366, a2 = 2598.63.
We use the quadratic equation to calculate the integral between V1 and V2:
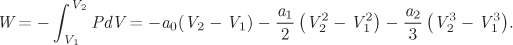
Using the fitted parameters and V1 = 0.1386 m3/kg, V2 = 0.06647 m3/kg, we find
W = 1.998 bar m3/kg = 199.8 kJ/kg.
Figure 3-4 shows the data and the fitted line. In this case both methods give nearly identical results because the tabulation includes closely spaced points.
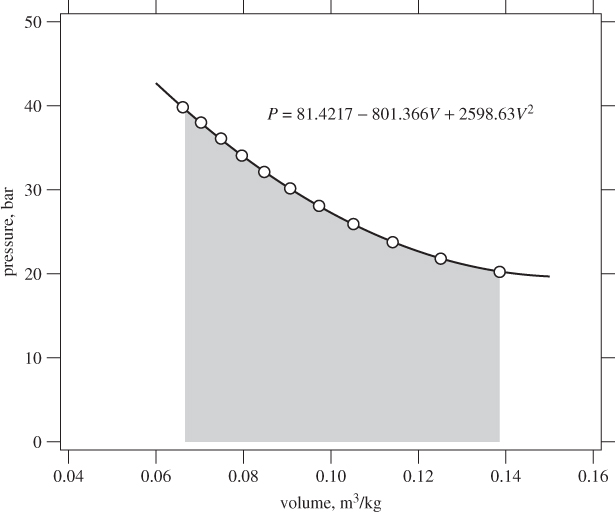
Figure 3-4: Calculation of isothermal PV work at 350 °C from steam tables. The solid line is a quadratic fit to the points from the tables (see Example 3.3).
3.3 Internal Energy and Heat
Molecules possess energy of various forms. All molecules possess kinetic energy due to the motion of the center of mass in space (translational kinetic energy). In addition to translational kinetic energy, polyatomic molecules possess rotational kinetic energy, manifested as motion relative to the center of mass, and vibrational energy, as motion of the constituent atoms relative to the equilibrium length of their chemical bonds. Molecules also possess potential energy as a result of interactions between different molecules as well as between atoms of the same molecule. These interactions can be loosely visualized as springs whose compression or extension requires energy.2 For our purposes it is not necessary to consider these molecular modes of energy storage in any detail. It suffices to say that matter, regardless of chemical composition or phase, is capable of storing energy internally. We refer to these combined storage modes as internal energy and we will use the symbol U. Like all forms of energy, internal energy is a state function and for a pure substance, it is a function of pressure and temperature.
2. To apply the spring analogy to intermolecular interactions we imagine the spring constant to be variable with distance: the intermolecular spring stiffens when highly compressed but becomes very soft when it is overextended.
The molecular nature of matter gives rise to a different type of energy transfer, heat. The mean kinetic energy of molecules in a hot substance is higher than that in a cold substance. The nature of molecular collisions is such, that when molecules with low kinetic energy are mixed with molecules of higher energy, energy is exchanged in a way that gives all molecules the same energy on average. The effect of collisions then is to spread the energy among molecules, much like the cue ball distributes its energy among all balls on a pool table. This process amounts to transferring energy from “hot” molecules to “cold” ones. Collisional transfer of energy does not require intimate mixing and it can take place when two solids are placed into contact, or when two fluids come into contact with a common solid wall. Molecules in the solid phase, though restricted in the range of their motion, move vigorously about their equilibrium position and collide with their neighbors, thus absorbing energy from higher-energy molecules and transferring it to those with lower energy. The rate of this transfer varies among materials, but this affects only how long it takes to reach equilibrium, not the final equilibrium itself. A thermal insulator, we may note here, is a material that offers a resistance to heat transfer so that the amount transferred over the duration of a typical application is negligibly small. Over time, however, heat will escape, even through an insulator, and thermal equilibrium will be established across all systems that are in contact with each other.
Heat shares some important characteristics with work:
1. It is a transient form of energy that is observed during a change of state (process); once the system is in equilibrium with its surroundings there is no net heat transfer because both system and surroundings are at the same temperature.3
3. On an instantaneous basis, individual collisions may transfer energy in either direction, from the system to the bath or the other way around, even at equilibrium. Overall, however, there is no net transfer between system and surroundings if the conditions of thermal equilibrium are met.
2. As a transient form, heat is not a storable mode of energy: once it enters a system, it is stored as internal energy. It is incorrect to say that a system “contains heat,” or to speak of energy that “is converted into heat.”
3. It has a direction, from the system to the surroundings, or vice versa.
4. It is a path function whose value is determined by the entire path of the process. This property of heat is not obvious at the moment but will become so in the next section.
Sign convention for heat: Heat is positive if it is transferred to the system from the surroundings, negative if it is transferred from the system to the surroundings.
Leave a Reply