Elementary Paths

Constant-Volume Heating

Consider the process in which a closed system is heated under constant volume. There is no PV work because the volume of the system is fixed. We assume there is no shaft work either. Then, the first law gives,

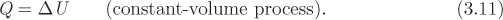
Therefore, the amount of heat that is exchanged under constant volume is equal to the change of internal energy, provided that no shaft work is present. Recall that shaft work, if present, will be made obvious through the presence of mechanical devices such as impellers, pumps, compressors, turbines, and the like. If a problem makes no mention of any such devices, it will be assumed that no shaft work is involved, without explicitly stating this assumption each time.

Example 3.5: Constant-Volume Cooling

A sealed metal cylinder contains steam at 1 bar, 500 °C. How much heat must be removed at constant volume in order to produce saturated vapor?

Solution Outline: This is a constant-volume process; therefore, the heat is equal to the change of internal energy between the initial (A) and final (B) state:

Q = U_B − U_A.

The initial state is known. In the final state we know the specific volume (must be equal to the specific volume in the initial state) and that the state is saturated vapor. These two pieces of information are sufficient to fix the final state. Once the final state is known, the heat is calculated by the above equation.

Numerical substitutions: From the steam tables at the initial state we read:

V_A = 3.5656 m³/kg, U_A = 3132.2 kJ/kg.

At the final state water is saturated vapor with V_B = V_A = 3.5656 m³/kg. The desired temperature is between 78 °C and 80 °C. By interpolation we find:

T_B = 78.8 °C, U_B = 2480.1 kJ/kg.

The amount of heat that must be exchanged with the surroundings is

Q = U_B − U_A = (2480.1 − 3132.2) kJ/kg = − 652.1 kJ/kg.

It is negative; therefore, it represents cooling.

Constant-Pressure Heating

A common way to exchange heat is under constant pressure. The expansion/ contraction of volume that accompanies heating/cooling involves the exchange of PV work with the surroundings, and this must be accounted for in the energy balance. We assume that the PV work is exchanged reversibly. Experimentally, this means that heat must be added or removed at a gentle rate to allow temperature to equilibrate and the expansion or contraction to take place in an controlled manner. Applying eq. (3.4) and noting that pressure is constant, the work is

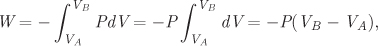
with subscripts A and B referring to the initial and final state, respectively. Substituting this result in eq. (3.9) and solving for the heat, we find,

ΔU_AB = Q − P(V_B − V_A) ⇒ Q = (U_B + PV_B) − (U_A + PV_A).

In the last result, the right-hand side is the difference of the term U + PV evaluated at the final state B, and the same term evaluated at the initial state A (recall that P_B = P_A = P for this process). This grouping of state functions is itself a state function. This motivates the definition of a new thermodynamic property, enthalpy:

Using this definition, the heat in constant-pressure process is

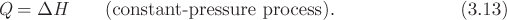
Therefore, in constant-pressure heating of a closed system, the amount of heat that is exchanged is equal to the change in enthalpy. Enthalpy is a state function and has the same units as internal energy (kJ/kg or J/mol). It is the relevant thermodynamic in the energy balance of open systems, as we will see in Chapter 6. As the large majority of chemical processes involves open systems, such as units with multiple inlet and outlet flow streams, enthalpy is used far more than internal energy and is tabulated more extensively. In fact, tabulations of internal energy are uncommon because it can be calculated from tabulations of enthalpy and volume.

Example 3.6: Enthalpy of Steam

Use the steam tables to obtain the enthalpy of steam at 1 bar, 300 °C, and compare the value calculated by application of the definition, eq. (3.12).

Solution From the steam tables at P = 1 bar, T = 300 °C, we find

H = 3074.5 kJ/kg.

At the same pressure and temperature we also find

V = 2.6389 m³/kg, U = 2810.7 kJ/kg.

To apply eq. (3.12) we first calculate the product PV:

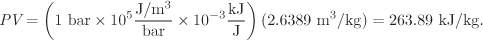
The enthalpy calculated from eq. (3.12) is

H = U + PV = (2810.7 kJ/kg) + (263.89 kJ/kg) = 3074.54 kJ/kg.

The calculated value agrees with the tabulated value within the precision of the table. Small round-off errors should be expected due to truncation in the tables.

Example 3.7: Constant-Pressure Cooling of Steam

8.5 kg of steam at 600 °C, 15 bar, are cooled at constant pressure by removing 6200 kJ of heat. Determine the final temperature and the amount of PV work that is exchanged with the surroundings.

Solution To specify the final state we need two intensive variables. The final pressure is known since it is constant during the process and equal to the initial pressure. The missing piece of information is the enthalpy of the final state, which will be obtained by energy balance.

For constant-pressure heating, Q = H₂ − H₁, which solved for H₂ gives

H₂ = H₁ + Q.

The amount of heat, per kg of steam, is

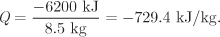
From the steam tables at the initial state,

P₁ = 15 bar, T₁ = 600 °C: U₁ = 3294.5 kJ/kg, H₁ = 3694.6 kJ/kg.

The final enthalpy is now calculated to be

H₂ = H₁ + Q = 3694.6 kJ/kg + (−729.4) kJ/kg = 2965.2 kJ/kg.

In the final state we know pressure (P₂ = P₁ = 15 bar) and enthalpy (H₂ = 2965.2 kJ/kg). By inspection in the steam tables at P = 15 bar, the final temperature must be between 250 °C and 300 °C. The exact temperature is obtained by interpolation:

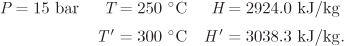
By interpolation at H = H₂ = 2965.2 kJ/kg,

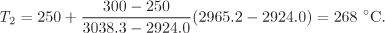
To calculate the work, we use eq. (3.9):

Since pressure and temperature are known at the final state, the internal energy is obtained directly from the table. This requires one additional interpolation:

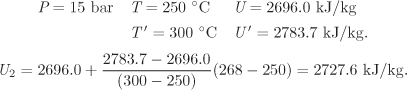
Finally, the work is

W = 2727.6 − 3294.5 −(−729.4) = 162.5 kJ/kg.

The work calculated here is per kg of steam. The total amount of work for the entire amount of steam is W = (8.5 kg)(162.5 kJ/kg) = 1381.4 kJ. The work is positive, which means, it is done by the surroundings and is absorbed by the system.

Example 3.8: Work and Heat are Path Functions

Steam undergoes the following reversible process in a closed system: from initial conditions 10 bar, 400 °C, to 550 °C under constant pressure, then to 8 bar under constant volume. Determine the energy balances. How would the energy balances change if steam from the same initial state were first cooled at constant volume to 8 bar, then heated at constant pressure to the same final state?

Solution The process is shown by the path 1 → 2 → 3 in Figure 3-6. The properties for states 1 and 2 are obtained directly form the steam tables; the state at 3 requires interpolation. The information is summarized in the table below:

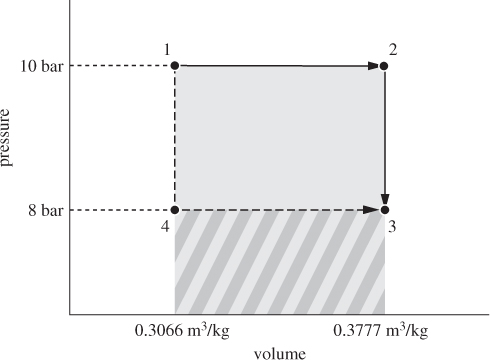
Figure 3-6: Energy balances along different paths (Example 3.8).

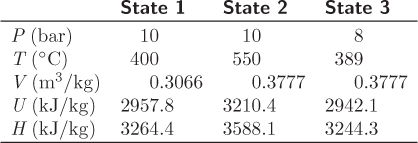
The energy balances are performed along each branch separately.

1 → 2: In this constant-pressure segment, heat is equal to the enthalpy change:

Q₁₂ = H₂ − H₁ = (3588.1 − 3264.4) kJ/kg = 323.7 kJ/kg.

The amount of heat is positive, i.e., the system is being heated. The work is given by eq. (3.4), which for a constant-pressure process is

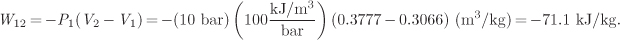
This work is produced by the system as a result of expanding against the surroundings.

2 → 3: In this segment volume is constant. The heat is equal to the change of internal energy:

Q₂₃ = U₃ − U₂ = (2942.1 − 3210.4) kJ/kg = −268.3 kJ/kg.

No PV work is exchanged:

W₂₃ = 0 kJ/kg.

Entire process: 1 → 2 → 3: The results are summarized in the table below:

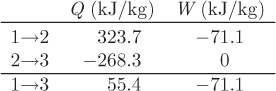
Overall balance: The change in internal energy between the initial and final states is

ΔU₁₃ = U₃ − U₁ = (2942.1 − 2957.8) kJ/kg = −15.7 kJ/kg.

This is equal to the sum of heat and work:

Q₁₂₃ + W₁₂₃ = 55.4 + (−71.1) = −15.7 kJ/kg.

Alternate Path When the process is conducted by first applying a constant-V path followed by a constant-pressure one, the combined path is the one marked as 1 → 4 → 3 in Figure 3-6. The calculation can be done by following the same procedure as with the previous path. However, the calculation can be simplified by noting that several required quantities have computed already.

The change in internal is the same as in the previous case since the initial and final states are the same:

ΔU₁₃ = U₃ − U₁ = (2942.1 − 2957.8) kJ/kg = −15.7 kJ/kg.

The work corresponds to the area under the path and is calculated as

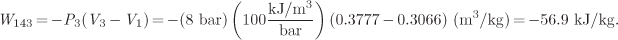
The heat is calculated by application of the first law:

Q₁₄₃ = ΔU₁₃ − W₁₄₃ = −15.7 kJ/kg − (−56.9) kJ/kg = 41.2 kJ/kg.

The results for the two cases are summarized below:

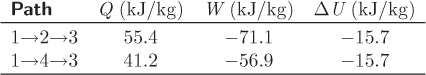
Comments

• Internal energy is a state function: Its difference between two states is determined by the states alone and not by the path that is used to connect these states.

• Work and heat are path functions: Their value depends on the entire path that connects two states.

• That work is a path function is demonstrated by the fact that work corresponds to the area under the path. Clearly, the path 1 → 2 → 3 involves more work because it covers a larger area. Since the sum of work plus heat is independent of the path (it is equal to the change of the internal energy), we conclude that heat must be a path function as well.