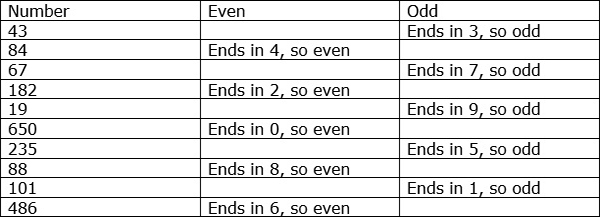
Definitions

Prime numbers

A number is a prime number if its only factors are 1 and itself.

7 is a prime number. Its factors are 1 and 7 itself

Some examples of prime numbers are 2, 3, 5, 7, 11, 13 and so on.

2 is the only even prime number. All other prime numbers are odd numbers

Composite numbers

If a number has three or more factors, it is a composite number. A number which has factors in addition to one and itself is called a composite number.

6 is a composite number. It has four factors; 1, 2, 3 and 6

For example: 4, 6, 8, 9, 10, 12,…are examples of some composite numbers

All even numbers except 2 are composite numbers.Neither Prime nor Composite

0 and 1 are neither prime numbers nor composite numbers.Problem 1:

State whether each number in table below is prime or not.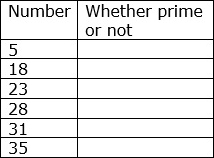

Solution

Step 1: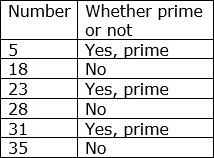

Step 2:

Of the given numbers 18, 28 and 35 have three or more factors. So they are not prime but composite numbers.

Step 3:

The numbers 5, 23 and 31 have only 1 and themselves as factors. So these numbers are prime numbers.Problem 2:

State whether each number in table below is prime or not.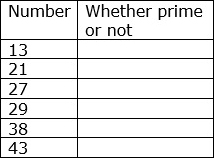

Solution

Step 1: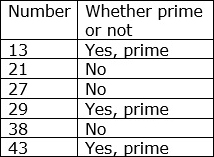

Step 2:

Of the given numbers 21, 27 and 38 have three or more factors. So they are not prime but composite numbers.

Step 3:

The numbers 13, 29 and 43 have only 1 and themselves as factors. So these numbers are prime numbers.

Divisibility Rule for 3

If the sum of the digits of a number is divisible by 3, then the number is divisible by 3.

Some examples of numbers divisible by 3 are as follows.

• The number 85203 is divisible by 3 because the sum of its digits 8+5+2+0+3=18 is divisible by 3.
• The number 79154 is not divisible by 3 because the sum of its digits 7+9+1+5+4=26 is not divisible by 3.

Divisibility Rule for 9

If the sum of the digits of a number is divisible by 9, then the number is divisible by 9.

Some examples of numbers divisible by 9 are as follows.

• The number 51984 is divisible by 9 because the sum of its digits 5+1+9+8+4=27 is divisible by 9.
• The number 91403 is not divisible by 9 because the sum of its digits 9+1+4+0+3=17 is not divisible by 9.

Problem

Find the divisibility of the numbers in following table

Solution

Definition

Divisibility − A number m is said to be divisible by another number n

if n divides m completely without leaving a remainder.

Divisibility Rule for 2

• If a number ends in a 0, 2, 4, 6 or 8, it is divisible by 2.
• All even numbers, by definition, are divisible by 2.

Some examples of numbers divisible by 2 are as follows.

24, 18, 68, 108, 184, 1020.

Divisibility Rule for 5

• If a number ends in either a 0 or 5, it is divisible by 5.

Some examples of numbers divisible by 5 are

15, 35, 75, 125, 505, 1000.

Divisibility Rule for 10

• If a number ends in a 0, it is divisible by 10.
• Also if a number is divisible by both 2 and 5, it is divisible by 10.

Some examples of numbers divisible by 10.

20, 50, 90, 110, 170, 1200.Problem :

Find the divisibility of the numbers in following table −

Solution

Even numbers

Even numbers are those numbers that are divisible by 2

All those numbers that have a 0, 2, 4, 6 or 8 in their ones place are even numbers.

For example, 4, 16, 38, 464, 1070are even numbers as they are divisible by 2

Odd numbers

Odd numbers are those numbers that are NOT divisible by 2.

All those numbers that have a 1, 3, 5, 7 or 9 in their ones place are odd numbers.

For example, 3, 7, 19, 75, 697, 3743are all odd numbers.Problem 1

For each of the numbers below, select even or odd.

Solution

This tutorial provides comprehensive coverage of prime numbers, factors and multiples based on Common Core CCSS and State Standards and its prerequisites. Students can navigate learning paths based on their level of readiness. Institutional users may customize the scope and sequence to meet curricular needs. This simple tutorial uses appropriate examples to help you understand prime numbers, factors and multiples in a general and quick way.

Audience

This tutorial has been prepared for beginners to help them understand the basics of prime numbers, factors and multiples. After completing this tutorial, you will find yourself at a moderate level of expertise in prime numbers, factors and multiples, from where you can advance further.

Prerequisites

Before proceeding with this tutorial, you need a basic knowledge of elementary math concepts such number sense, addition, subtraction, multiplication, division, multiplication facts, tables, multiples and factors of numbers and so on.