Category: Prime Numbers Factors and Multiples

Using Prime Factors to Find the Least Common Multiple of Two Numbers

• The two numbers are written as products of their prime factors.
• The product of the maximum occurrences of each prime factor in the numbers gives the least common multiple of the two numbers.

Example

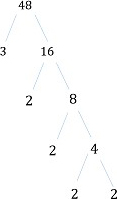
Find least common multiple lcm of 21 and 48

Solution

Step 1:

The prime factors of 21 and 48 are 21 = 3 7

48 = 2 2 2 2 3

Step 2:

Maximum occurrences of the prime factors are 24times; 31time; 71time

Step 3:

Least common multiple of 21 and 48 = 2 2 2 2 3 7 = 336Problem 1:

A bell rings every 18 seconds, another every 60 seconds. At 5.00 pm the two ring simultaneously. At what time will the bells ring again at the same time?

Solution

Step 1:

A bell rings every 18 seconds, another every 60 seconds

Prime factorizations of 18 and 60 are

18 = 2 3 3

60 = 2 2 3 5

Step 2:

LCM is the product of maximum occurrences of each prime factor in the given numbers.

Step 3:

So L C M 12,18 = 2 2 3 3 5 = 180 seconds = 180/60 = 3 minutes.

So the bells will ring at same time again at 5.03pmProblem 2:

A salesman goes to New York every 15 days for one day and another every 24 days, also for one day. Today, both are in New York. After how many days both salesman will be again in New York on same day?

Solution

Step 1:

A salesman goes to New York every 15 days and another every 24 days

Prime factorizations of 15 and 24 are

15 = 3 5

24 = 2 2 2 3

Step 2:

LCM is the product of maximum occurrences of each prime factor in the given numbers.

Step 3:

So L C M 12,18 = 2 2 2 3 5 = 120 days.

So both salesmen will be in New York after 120 days.Problem 3:

What is the smallest number that when divided separately by 20 and 48, gives the remainder of 7 every time?

Solution

Step 1:

Prime factorizations of 20 and 48 are

20 = 2 2 5

48 = 2 2 2 2 3

Step 2:

LCM is the product of maximum occurrences of each prime factor in the given numbers.

Step 3:

So L C M 20,48 = 2 2 2 2 3 5 = 240

The required number is 240 + 7 = 247

Introduction

Finding the least common multiple lcm of three numbers is similar to finding the lcm of 2 numbers.

To find the least common multiple lcm of three numbers

• We begin by listing the first few multiples of the three numbers.
• Then we look for the common multiples of all the numbers.
• The first common multiple of the numbers would be their least common multiple.

Problem 1:

Find the least common multiple of 6, 10, 15

Solution

Step 1:

The multiples of 6, 10 and 15 are as follows

Multiples of 6 = 6, 12, 18, 24, 30, 36, 42, 48, 54, 60

Multiples of 10 = 10, 20, 30, 40, 50, 60, 70, 80

Multiples of 15 = 15, 30, 45, 60, 75, 90

Step 2:

Some common multiples of the three numbers are 30, 60…

Step 3:

The first common multiple of 6, 10 and 15 is 30, which is their least common multiple lcmProblem 2:

Find the least common multiple of 9, 12, 24

Solution

Step 1:

The multiples of 9, 12 and 24 are as follows

Multiples of 9 = 9, 18, 27, 36, 45, 54, 63, 72

Multiples of 12 = 12, 24, 36, 48, 60, 72

Multiples of 24 = 24, 48, 72, 96

Step 2:

The first common multiple of 9, 12 and 24 is 72, which is their least common multiple lcm

Definitions

The multiple of a number is that number multiplied by an integer. The multiples of a number are found by multiplying it with 1, 2, 3, 4….and so on.

For example, the multiples of 4 are 4 × 1, 4 × 2, 4 × 3, 4 × 4,…or 4, 8, 12, 16 …and so on.

The multiples of two numbers that are common to both the numbers are known as common multiples of those numbers.

The smallest positive number that is a common multiple of two numbers is the least common multiple or lcm of those two numbers.

The least common mulitple of two numbers is also the smallest number that both the numbers divide completely without leaving a remainder.

Rules to find the least common multiple of two numbers

• We begin by listing the first few multiples of the two numbers.
• Then we look for the common multiples of both the numbers.
• The first common multiple of the numbers would be their least common multiple.

Example

Find the least common multiple of 8 and 10

Solution

Step 1:

The multiples of 8 and 10 are as follows

Multiples of 8 = 8, 16, 24, 32, 40, 48, 56, 64, 72, 80…

Multiples of 10 = 10, 20, 30, 40, 50, 60, 70, 80…

Step 2:

The first common multiple of 8 and 10 is 80, which is their least common multiple lcmProblem 1:

Find the least common multiple of 12 and 18

Solution

Step 1:

The multiples of 12 and 18 are as follows

Multiples of 12 = 12, 24, 36 , 48, 60, 72, 84…

Multiples of 18 = 18, 36, 54, 72, 90, 108…

Step 2:

The first common multiple of 12 and 18 is 36, which is their least common multiple lcmProblem 2:

Find the least common multiple of 9 and 15

Solution

Step 1:

The multiples of 9 and 15 are as follows

Multiples of 9 = 9, 18, 27, 36, 45, 54…

Multiples of 15 = 15, 30, 45, 60…

Step 2:

The first common multiple of 9 and 15 is 45, which is their least common multiple lcm

Introduction

We can have sums or differences of whole numbers; for example 26+65 or 48−16.

For factoring such sums or differences of whole numbers:

• We write the whole numbers as products of their prime factors.
• Then we factor out the greaterst common factors gcf from those numbers
• We factor out any given common factor, if required, from such sums or differences of whole numbers.

Example:

Factor out the gcf from the sum 28+63

Solution

The prime factorization of 28 is 28 = 4 × 7

The prime factorization of 63 is 63 = 9 × 7

So the greatest common factor or gcf of 28 and 63 is 7

So 28+63 = 4×7+9×7 = 74+9Problem 1:

Factor out the gcf from the sum of whole numbers 26+91

Solution

Step 1:

26 = 2 13

91 = 7 13

Step 2:

The gcf of 26 and 91 is 13. So factoring out the greatest common factor 13

26+91 = 213+713= 132+7Problem 2:

Factor out 6 from the difference of whole numbers 10884

Solution

Step 1:

84 = 2 2 3 7 = 6 14

108 = 2 2 3 3 3 = 6 18

Step 2:

So factoring out 6 from the difference of the given numbers

10884 = 618614 = 61814

This lesson is designed to explore decomposition, multiplication, and factoring of whole numbers and the distributive property.Problem 1:

Factor out a common factor of 5 from 45.

Solution

Step 1:

The expanded form of 45 is written as follows

45 = 40 + 5

Step 2:The common factor of 5 and 40 is 5 itself.

Step 3:

Using distributive property to factor out the common factor 5

45 = 40+5 = 5×8+5×1 = 58+1Problem 2:

Given a number 36

i Factor out a common factor of 2

ii Factor out a common factor of 6

Solution

Step 1:

The expanded form of given number is written as follows

36 = 30 + 6

Step 2:

Using distributive property

i Factoring out a common factor of 2

36 = 30 + 6 = 2 × 15 + 2 × 3 = 215+3

Step 3:

Using distributive property

ii Factoring out a common factor of 6

36 = 30 + 6 = 5 × 6 + 1 × 6 = 65+1

Introduction

When multiplying a number by a sum or difference, we use the distributive property.

The distributive property states that for any three numbers ‘a’, ‘b’ and ‘c’

• a b+c = ab + ac
• a b−c = ab − ac

For example, in the math statement 7 4+9, we are multiplying 7 with a sum of 4 and 9. Here we can use the distributive property as follows.

7 4+9 = 74 + 79 = 28 + 63 = 91

Similarly, in the math statement 5 83, we are multiplying 5 with a difference of 8 and 3. Here we can use the distributive property as follows.

5 83 = 58 53 = 40 15 = 25

In an expression for example, 6 3+5, we can simplify using the order of operations rule PEMDAS or use distributive property.

If  PEMDAS rule is followed

6 3+5 = 6 8 = 48

Wesimplifytheparenthesesfirstandthendomultiplicationoperationnext

If distributive property is used

6 3+5 = 63 + 65 = 18 + 30 = 48

Either way, the answer is the same.

Sometimes it is easier to use the distributive property to simplify than using the order of operations rule PEMDAS.Problem

Simplify 4 3+50 using distributive property

Solution

Step 1:

In 4 3+50, it is easier to simplify using distributive property as follows

4 3+50 = 43 + 450 = 12 + 200 = 212

Step 2:

If PEMDAS rule is used

4 3+50 = 4 53 = 212

Definition

The distributive property states that when we multiply a factor and a sum or difference, we multiply the factor by each term of the sum or difference.

Formula

The distributive property of multiplication for any three real numbers ‘a’, ‘b’ and ‘c’ is

• a × b + c = a×b + a×c
• a × b−c = a×b − a×c

Example

Rewrite 8 × 7 + 4 using distributive property in order to simplify

Solution

Step 1:

According to distributive property for any three real numbers, ‘a’, ‘b’ and ‘c’

a × b + c = a×b + a×c

Step 2:

8 × 7 + 4 = 8×7 + 8×4 = 56 + 32 = 88Problem 1:

Rewrite given expression using distributive property in order to simplify

8 × 7 + 4

Solution

Step 1:

According to distributive property for any three real numbers, ‘a’, ‘b’ and ‘c’

a × b + c = a×b + a×c

Step 2:

8 × 7 + 4 = 8×7 + 8×4 = 56 + 32 = 88Problem 2:

Rewrite given expression using distributive property in order to simplify

9 × 6−2

Solution

Step 1:

According to distributive property for any three real numbers, ‘a’, ‘b’ and ‘c’

a × b−c = a×b − a×c

Step 2:

9 × 6−2 = 9×6 − 9×2 = 54 − 18 = 36

Introduction

Given three numbers, the method of finding greatest common factor is same as the method of finding gcf of two numbers.

• We list all the factors of the three numbers.
• We look for the common factors of these numbers.
• Among these we find for the greatest number which will be the gcf of the three given numbers.

Problem 1:

Find the greatest common factor of 18, 24 and 36

Solution

Step 1:

The factors of 18 and 24 and 36 are

18 = 1, 2, 3, 6, 9, 18

24 = 1, 2, 3, 4, 6, 8, 12, 24

36 = 1, 2, 3, 4, 6, 9, 12, 18, 36

Step 2:

The common factors of 18, 24 and 36 are shown in bold.

Step 3:

The greatest among these is 6. So the greatest common factor gcf of 18, 24 and 36 is 6.Problem 2:

Find the greatest common factor of 15, 35 and 75

Solution

Step 1:

The factors of 15, 35 and 75 are

15 = 1, 3, 5, 15

35 = 1, 5, 7, 35

75 = 1, 3, 5, 15, 25, 75

Step 2:

The common factors of 15, 35 and 75 are shown in bold.

Step 3:

The greatest among these is 5. So the greatest common factor gcf of 15, 35 and 75 is 5.

Introduction

To find the greatest common factor gcf of two given numbers,

• First we list all the factors of the two numbers.
• Then, we look for the common factors of these numbers.
• We find the greatest number among these common factors which will be the greatest common factor gcf of the two given numbers.

Problem 1:

Find the greatest common factor of 16 and 24.

Solution

Step 1:

The factors of 16 and 24 are

16 = 1, 2, 4, 8, 16

24 = 1, 2, 3, 4, 6, 8, 12, 24

Step 2:

The common factors of 16 and 24 are shown in bold.

Step 3:

The greatest among these is 8. So the greatest common factor gcf of 16 and 24 is 8.Problem 2:

Find the greatest common factor of 84 and 108.

Solution

Step 1:

The factors of 84 and 108 are

84 = 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84

108 = 1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54, 108

Step 2:

The common factors of 84 and 108 are shown in bold.

Step 3:

The greatest among these is 12. So the greatest common factor gcf of 84 and 108 is 12.

Definitions

Factors are the numbers we multiply to get another number.

For example, factors of 14 are 2 and 7, because 2 7 = 14.

Some numbers can be factored in more than one way.

For example, 16 can be factored as 1 16, 2 8, or 4 4.

A number that can only be factored as 1 times itself is called a prime number.

The first few primes are 2, 3, 5, 7, 11, and 13.

Numbers which have multiple factors are called composite numbers.

The number 1 is neither a prime nor a composite number.

We can write any whole number as a product of two factors and start a factor tree. The factors are further broken down into their factors till we are left with only prime factors which cannot be further broken down.

You most often are required to find the prime factors of a number: the list of all the prime-number factors of a given number.

The factorization of a number into its prime factors and expression of the number as a product of its prime factors is known as the prime factorization of that number.

The prime factorization of a number includes ONLY the prime factors, not any products of those prime factors.

Example

Find the prime factors of 24

Solution

Step 1:

To find prime factors of 24, you divide it by the smallest prime number that divides it evenly: 24 ÷ 2 = 12.

Step 2:

Now divide 12 by the smallest prime number that divides evenly: 12 ÷ 2 = 6.

Step 3:

Now divide 6 by the smallest prime number that divides it evenly: 6 ÷ 2 = 3.

Step 4:

Since 3 is prime, factoring is completed, and the prime factorization of 24 is 2 2 2 3.Problem 1:

Find all the prime factors of 48.

Solution

Step 1:

We can breakdown 48 into its factors as shown below.

48 = 3 16;

16 = 2 8;

8 = 2 4;

4 = 2 2.

Step 2:

The factor tree we get here is shown below.

Step 3:

So 48 written as a product of its prime factors or prime factorization of 48 is

48 = 2 2 2 2 3Problem 2:

Find all the prime factors of 75.

Solution

Step 1:

We can breakdown 75 into its factors as shown below.

75 = 3 25;

25 = 5 5;

Step 2:

The factor tree we get here is shown below.

Step 3:

So 75 written as a product of its prime factors or the prime factorization of 75 is

75 = 3 5 5