Category: Multiply and Divide Decimals

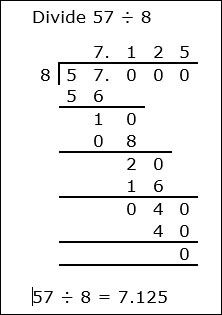
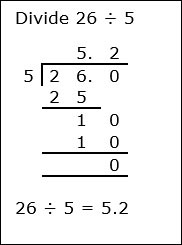Definition

Average is a number that represents a group of numbers. It is calculated by adding up all the numbers, then dividing the total by the count of numbers.

In other words, it is the sum divided by the count.

Average of two numbers is given by the sum of the two numbers divided by two.

Formula

The average of two numbers is given by x = (a + b)/2 where x is the average a and b are any two numbers.

Problem 1

What is the average of the numbers 6 and 18?

Solution

Step 1:

Adding the numbers: 6 + 18 = 24

Dividing by 2: 24 / 2 = 12

Step 2:

The average of the two numbers 6 and 18 is 12

Problem 2

If the average of 19 and q is 27, what number is q?

Solution

Step 1:

The average of 19 and q = 19+q/2 = 27

19 + q = 27 2 = 54

q = 54 19 = 35

Step 2:

So, the number q is 35

Problem 3

If the average of two consecutive even numbers is 35, what are those numbers?

Solution

Step 1:

Let the consecutive even numbers be n and n+2

Their average is n+n+2/2 = 2n+2/2 = 35

2n+2 = 35 2 = 70

2n = 70 2 = 68; n = 68/2 = 34

Step 2:

So, the consecutive even numbers are 34 and 34+2 or 34 and 36

Definition

A power of 0.1 is 10 raised to a negative whole number as follows

0.1 = 10¹; 0.1² = 10² = 0.01; 0.1³ = 10³ = 0.001 and so on.

A power of a 0.1 has one preceded by zeros with as many decimal places as the power of 0.1. For example, 0.1² is equal to 0.01 which has as many decimal places 2 as the power of 0.1 which is 2.

Formula

The quotient of a decimal divided by a power of 0.1 can be found by a short cut. When a decimal number is divided by a power of 0.1, the quotient is found by moving the decimal point to the right that many places as the power of 0.1

Problem 1

Divide 36.193 ÷ 0.1²

Solution

Step 1:

36.193 ÷ 0.1²

Here the power of 0.1 is two or there are two decimal places in its value 0.01.

Step 2:

So the decimal point in 36.193 is moved 2 places to the right and the quotient is obtained as shown below.

36.193 ÷ 0.1² = 36.193 ÷ 0.01 = 3619.3

Problem 2

Divide 41.15 ÷ 0.1³

Solution

Step 1:

41.15 ÷ 0.1³

Here the power of 0.1 is three or the number of decimal places in its value 0.001 is 3.

Step 2:

So the decimal point in 45.15 is moved 3 places to the right and the quotient is obtained as shown below. A zero is added after 1 to make three places shift to the right.

41.15 ÷ 0.1³ = 41.15 ÷ 0.001 = 41150

Definition

A power of ten is 10 raised to a whole number.

For example, 10¹ = 10; 10² = 100; 10³ = 1000 and so on.

A power of a ten has one followed by as many zeros as the power. For example, 10² is equal to one followed by two zeros, i.e., 100.

Formula

The quotient of a decimal divided by a power of ten can be found by a short cut.When a decimal number is divided by a power of ten, the quotient is found by moving the decimal point to the left that many places as the number of zeros in the power of ten.

Problem 1

Divide 8.234 10²

Solution

Step 1:

8.234 10²

Here the power of ten is two or the number of zeros in its value 100 is 2.

Step 2:

So the decimal point in 8.234 is moved 2 places to the left and the quotient is obtained as shown below.

8.234 10² = 8.234 100 = 0.08234

Problem 2

Divide 14.76 10³

Solution

Step 1:

14.76 10³

Here the power of ten is three or the number of zeros in its value 1000 is 3.

Step 2:

So the decimal point in 14.76 is moved 3 places to the left and the quotient is obtained as shown below.

14.76 10³ = 14.76 1000 = 0.01476

Introduction

Division of a decimal by a decimal is similar to whole number division.

Rules for Decimal Division

• First we make both the decimals have the same number of decimal places if required.
• Then we divide them as if they were whole numbers ignoring the decimal points.
• The quotient so obtained is the required answer.

Problem 1

Divide 96.2 ÷ 0.52

Solution

Step 1:

96.2 has one decimal place. 0.52 has two decimal places. So we make 96.2 have two decimal places by putting a zero to the right of 2 to make it 96.20.

Step 2:

Moving the decimal point to the right two places in both the numbers, it becomes a whole number division.

Now, 96.2 ÷ 0.52 = 96.20 ÷ 0.52 = 9620 ÷ 52 = 185

Problem – 2

Divide 9.36 ÷ 0.65

Solution

Step 1:

0.65 has two decimal places. 9.36 has two decimal places.

Step 2:

Now, 9.36 ÷ 0.65 = 936 ÷ 65 = 14.4

Introduction

Division of a decimal by a decimal is similar to whole number division.

Rules for Decimal Division

• First we make both the decimals have the same number of decimal places if required.
• Then we divide them as if they were whole numbers ignoring the decimal points.
• The quotient so obtained is the required answer.

Consider the following examples of division of a decimal by a 1-digit decimal

Problem 1

Divide 101.6 ÷ 0.8

Solution

Step 1:

101.6 has one decimal place. 0.8 has one decimal place. Here we move the decimal point to the right one place in both the numbers.

Step 2:

Now 101.6 ÷ 0.8 = 1016 ÷ 8 = 127

Problem 2

Divide 78.3 ÷ 0.9

Solution

Step 1:

Both 78.3 and 0.9 have one decimal place. Here we move the decimal point to the right one place in both the numbers.

Step 2:

Now 78.3 ÷ 0.9 = 783 ÷ 9 = 87

Print Page

Introduction

Division of whole numbers by whole numbers sometimes leaves remainders and such long division if continued results in decimal numbers as quotients.

Here we are dealing with examples of such whole number divisions with decimal quotients.

Problem 1

Solution

Problem 2

Solution

Problem 3

Solution

Problem 1

For first two days it snowed 2.6 centimeters each day. The next three days, it snowed 3.4 centimeters each day. How much did it snow on those five days?

Solution

Step 1:

Amount of snowfall on first two days

= 2 2.6

= 5.2 cm

Amount of snowfall on next three days

= 3 3.4

= 10.2 cm

Step 2:

Total snowfall in the five days

= 5.2 + 10.2

= 15.4 cm

Problem 2

Jamie ordered 7 pizzas and 8 burgers. Each pizza costs 12.85andeachburgercosts11.75. How much does she need to pay?

Solution

Step 1:

Cost of pizzas = 7 12.85 = $89.95

Cost of burgers = 8 11.75 = $94.00

Step 2:

Total amount to be paid = 89.95+94.00

= $183.95

Problem 1

Daniel earns $8.80 per hour at his part-time job. On Sunday, he worked 5.5 hours. What were his total earnings for the day?

Solution

Step 1:

Earnings per hour = $8.80

Number of hours worked = 5.5

Step 2:

Total earnings = 5.5 8.80 = $48.40

Problem 2

Nora ordered 9 pizzas. Each pizza costs $11.75. How much does she need to pay?

Solution

Step 1:

Cost of each pizza = $11.75

Number of pizzas = 9

Step 2:

Total amount spent = 9 11.75 = $105.75

Introduction

Multiplication of a decimal by another decimal is similar to whole number multiplication.

Rules for Multiplication of a Decimal by another Decimal

• In the multiplication of a decimal number by another decimal, we first multiply the numbers by ignoring the decimal point.
• We count the number of places of decimals in both the numbers and add.
• We then put the decimal point before as many places in the product from the right as the number obtained in step above.

In this lesson, we are solving problems that involve multiplication of decimals that have a product less than 0.1

Problem 1

Multiply 0.3 0.23

Solution

Step 1:

0.3 0.23

0.3 has one decimal place and 0.23 has two decimal places, so their product has three decimal places.

Step 2:

So, multiplying 0.3 0.23 = 0.069

The product is less than 0.1

Problem 2

Multiply 0.4 0.21

Solution

Step 1:

0.4 0.21

0.4 has one decimal place and 0.21 has two decimal places, so their product has three decimal places.

Step 2:

So, multiplying 0.4 0.21 = 0.084

The product is less than 0.1

Definition

A power of 0.1 is 10 raised to a negative whole number as follows

0.1 = 10¹; 0.1² = 10² = 0.01; 0.1³ = 10³ = 0.001 and so on.

A power of a 0.1 has one preceded by zeros with as many decimal places as the power of 0.1.
For example, 0.1² is equal to 0.01 which has as many decimal places 2 as the power of 0.1 which is 2.

Rules

The product of a decimal multiplied by a power of 0.1 can be found by a short cut. When a decimal number is multiplied by a power of 0.1, the product is found by moving the decimal point to the left that many places as the power of 0.1

Problem – 1

Multiply 27.43 0.1²

Solution

27.43 0.1²

Here the power of 0.1 is two and there are two decimal places in its value 0.01. So the decimal point in 27.43 is moved 2 places to the left and the product is obtained as shown below.

27.43 0.1² = 27.43 0.01 = 0.2743

Problem – 2

Multiply 16.26 0.1³

Solution

16.26 0.1³

Here the power of 0.1 is three and the number of decimal places in its value 0.001 is 3. So the decimal point in 16.26 is moved 3 places to the left and the product is obtained as shown below. A zero is added before 1 to make three places shift to the left.

16.26 0.1³ = 16.26 0.001 = 0.01626