Introduction

An electronic calculator displays fractions as decimal approximations rounded up to certain number 8,12oranyothernumber of places of decimals depending upon the company, type and model.

In this lesson, we learn how to use a calculator to convert a fraction to a rounded decimal.

Suppose we want the value of a fraction to be rounded to n places of decimal. We take the value with first n+1 digits after the decimal point from the calculator and round to n places i.e., we take one more digit than the required number of places of decimals. Then we round off the last digit. If the last digit is 5 or more, we add 1 to the preceding digit and if 4 or less we drop the last digit and write the first four digits as it is.

For example, suppose we want the value of a fraction to be rounded to four places of decimal. We take the value with first five digits after the decimal point from the calculator and round to four places i.e., we take one more digit than the required number of places of decimals. Then we round off the last digit. If the last digit is 5 or more, we add 1 to the preceding digit and if 4 or less we drop the last digit and write the first four digits as it is.

Example 1

Using a calculator convert 4785 into a decimal rounded to four places of decimal.

Solution

Step 1:

At first, we set up the fraction 4785 as a long division problem, dividing 47 by 85 using a calculator.

Step 2:

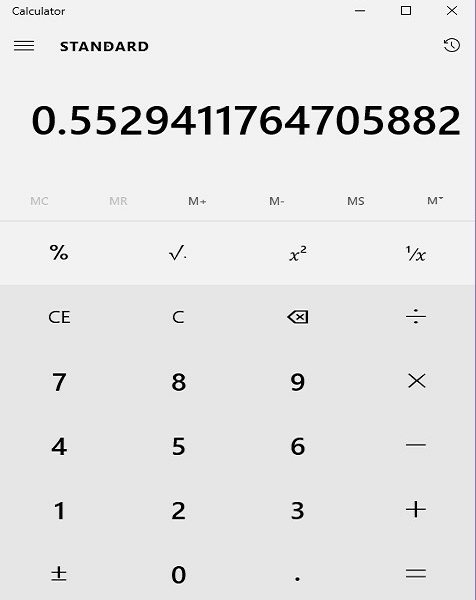
We find that on long division 4785=0.55294117…

Step 3:

Since we must round to four places of decimal, we consider the first five onemorethanfour digits after the decimal, i.e., 55294

Step 4:

The last digit is 4, so we drop it and keep the first four digits after the decimal only, i.e., 5529

Step 5:

So, 4785=0.5529

Example 2

Using a calculator convert 6744 into a decimal rounded to four places of decimal.

Solution

Step 1:

At first, we set up the fraction as a long division problem, dividing 67 by 44

Step 2:

We find that on long division 6744=1.522727272…

Step 3:

Since we must round to four places of decimal, we consider the first five onemorethanfour digits after the decimal, i.e., 52272

Step 4:

The last digit is 2, so we drop it and keep the first four digits after the decimal only, i.e., 5227

Step 5:

So, 6744=1.5227

Example 3

Using a calculator convert 8677 into a decimal rounded to four places of decimal.

Solution

Step 1:

At first, we set up the fraction as a long division problem, dividing 86 by 77

Step 2:

We find that on long division 8677=1.11688311…

Step 3:

Since we must round to four places of decimal, we consider the first five onemorethanfour digits after the decimal, i.e., 11688

Step 4:

The last digit is 8, so we add 1 to preceding digit which is also 8 to make it 9 and therefore rounding leads to, 1169

Step 5:

So, 8677=1.1169

Definition

A terminating decimal is a decimal that ends. In other words, a terminating decimal doesn’t keep going. It has a finite number of digits after the decimal point.

25=0.4;24=0.75;2516=1.5625

In the examples shown above, we have few fractions expressed as decimals. Notice that these decimals have a finite number of digits after the decimal point. So, these are terminating decimals.

Rule to convert a fraction to a terminating decimal

• To convert a fraction into a terminating decimal, the method is to set up the fraction as a long division problem to get the answer.

Here we are converting proper fractions into terminating decimals.

Example 1

Convert 34 into a decimal.

Solution

Step 1:

At first, we set up the fraction as a long division problem, dividing 3 by 4

Step 2:

We find that on long division 34=0.75 which is a terminating decimal.

OR

Step 3:

We write an equivalent fraction of 34 with a denominator 100.

34=(3×25)(4×25)=75100

Step 4:

Shifting the decimal two places to the left we get

75100=75.0100=0.75

Step 5:

So, 34=0.75 which again is a terminating decimal.

Example 2

Convert 2325 into a decimal.

Solution

Step 1:

At first, we can set up the fraction as a long division problem, dividing 23 by 25

Step 2:

We find that on long division 2325=0.92 which is a terminating decimal

OR

Step 3:

We write an equivalent fraction of 2325 with a denominator 100.

2325=(23×4)(25×4)=92100

Step 4:

Shifting the decimal two places to the left we get

92100=92.0100=0.92

Step 5:

So, 2325=0.92

Definition

A mixed number is a whole number and a proper fraction combined. So, a mixed number consists of two parts, the whole number part and the fractional part. For example, in mixed number 225 , the whole number part is 2 and the fractional part is 25.

In this lesson, we convert given mixed number with a denominator of 2, 4 or 5 into a decimal.

Rules to convert a mixed number with a denominator of 2, 4 or 5 into a decimal.

• At first, we convert a mixed number with a denominator of 2, 4 or 5 into a fraction using the algorithm method.
• Then, we write its equivalent fraction such that the denominator is a power of ten.
• We then shift the decimal that many places to the left as there are zeros after 1 in the denominator.

Example 1

Convert 212 into a decimal.

Solution

Step 1:

At first, we convert the mixed number into a fraction using the algorithm

212=(2×2+1)2=52

Step 2:

Then we write an equivalent fraction of 5/2 with a denominator 10.

52=(5×5)2×5=2510

Step 3:

Shifting the decimal one place to the left we get

2510=25.010=2.5

Step 4:

So, 212=2.5

Example 2

Convert 334 into a decimal.

Solution

Step 1:

At first, we convert the mixed number into a fraction using the algorithm

334=(3×4+3)4=154

Step 2:

Then we write an equivalent fraction of 15/4 with a denominator 100.

154=(15×25)(4×25)=375100

Step 3:

Shifting the decimal two places to the left we get

375100=375.0100=3.75

Step 4:

So, 334=3.75

Example 3

Convert 725 into a decimal.

Solution

Step 1:

At first, we convert the mixed number into a fraction using the algorithm

725=(7×5+2)5=375

Step 2:

Then we write an equivalent fraction of 37/5 with a denominator 10.

375=(37×2)(5×2)=7410

Step 3:

Shifting the decimal one place to the left we get

7410=74.010=7.4

Step 4:

So, 725=7.4

Definition

Proper fractions, are fractions where the numerator is smaller than the denominator. For example: 23,49,1113 are some proper fractions.

Some proper fractions have 2, 4 or 5 as their denominators.

There are certain shortcut methods for converting proper fractions with 2, 4 or 5 as denominators into decimals.

Rules for converting proper fractions with 2, 4 or 5 as denominators into decimals.

• At first, we write an equivalent fraction of given proper fraction with a denominator which is a power of ten.
• We then shift the decimal to as many places to the left as there are number of zeros after 1 in the denominator.

Example 1

Convert 12 into a decimal.

Solution

Step 1:

12 is a proper fraction of the type where the denominator is 2,4 or 5.

Step 2:

Here, we write an equivalent fraction of 12 with a denominator 10.

12=(1×5)(2×5)=510

Step 3:

Shifting the decimal one place to the left we get

510=5.010=0.5

Step 4:

So, 12=0.5

Example 2

Convert 34 into a decimal.

Solution

Step 1:

34 is a proper fraction of the type where the denominator is 2,4 or 5.

Step 2:

We write an equivalent fraction of 34 with a denominator 100.

34=(3×25)(4×25)=75100

Step 3:

Shifting the decimal two places to the left we get

75100=75.0100=0.75

Step 4:

So, 34=0.75

Example 3

Convert 25 into a decimal.

Solution

Step 1:

25 is a proper fraction of the type where the denominator is 2,4 or 5.

Step 2:

We write an equivalent fraction of 25 with a denominator 10.

25=(2×2)(5×2)=410

Step 3:

Shifting the decimal one place to the left we get

410=4.010=0.4

Step 4:

So, 25=0.4

Introduction

We should recall decimal place value charts. We know that, to the right of a decimal, the places values are the tenths, hundredths, thousandths and so on.

The rule says that the decimal point in the numerator shifts to the left as many places as the number of zeros after 1 in the denominator.

Consider here, fractions with denominators of 10 or 100

Rules to convert a fraction with a denominator of 10 to a decimal

• Suppose we have a fraction 710.
• At first, we write the numerator 7 only.
• Then we look at the denominator which is a ten which corresponds to the decimal place value tenth. So, 7 has a place value of a tenth. For this we put a decimal point before 7. So, 710 becomes the decimal .7 or 0.7
• Alternately, as the number of zeros in a 10 is 1, the decimal shifts one place to the left in 7 to make it 0.7

Rules to convert a fraction with a denominator of 100 to a decimal

• Next consider a fraction 97100.
• At first, we write the numerator 97 only.
• As we were dividing with a 100, we are looking at a place value of a hundredth. The digit 7 has a place value of a hundredth. So, a decimal point is put before 9 and we get 97100=.97 or 0.97.
• Alternately, as the number of zeros in a 100 is 2, the decimal point shifts two places to the left in 97 to make it 0.97

Example 1

Write 610 as a Decimal.

Solution

Step 1:

At first, we only write the numerator 6 as 6.0

Step 2:

Since the denominator 10 has a single zero, we shift the decimal point in 6.0 one place to the left and get .6 or 0.6 as the answer.

Step 3:

So, 610=0.6

Example 2

Write 48100 as a decimal.

Solution

Step 1:

At first, we write the numerator 48 as a decimal 48.0.

Step 2:

Since the denominator 100 has two zeros, we shift the decimal point in 48.0 two places to the left, and get the answer as .48 or 0.48

Step 3:

So, 48100=0.48

Introduction

Here a figure is given in the form of a circle or a rectangular strip or some other shape. It is then divided into certain number of equal parts. Some of these equal parts are shaded with colors.

Considering the figure as a one unit, it is required to find the fraction that represents the shaded region of the given figure.

It is also required to find the decimal representing the same shaded region.

Following examples will make it easy to write a fraction and a decimal that represent a shaded region in a figure.

Example 1

Write a decimal or fraction for the shaded region shown below.

Solution

Step 1:

Total parts of the circle = 3

Shaded parts of the circle = 2

Step 2:

Fraction representing shaded region of circle = 23

Step 3:

Writing the fraction as a repeating decimal 23=0.666=0.6¯

Example 2

Write a decimal or a fraction for the shaded region shown below.

Solution

Step 1:

Total parts of the rectangular strip = 5

Shaded parts of the strip = 1

Step 2:

Fraction representing shaded region of strip = 15

Step 3:

Writing the fraction as a decimal 15=210=0.2

Example 3

Write a decimal or fraction for the shaded region shown below.

Solution

Step 1:

Total parts of the circle = 5

Shaded parts of the circle = 4

Step 2:

Fraction representing shaded region of circle = 45

Step 3:

Writing the fraction as a decimal 45=810=0.8

This tutorial provides comprehensive coverage of converting fractions to decimals based on Common Core CCSS and State Standards and its prerequisites. Students can navigate learning paths based on their level of readiness. Institutional users may customize the scope and sequence to meet curricular needs. This simple tutorial uses appropriate examples to help you understand converting fractions to decimals in a general and quick way.

Audience

This tutorial has been prepared for beginners to help them understand the basics of converting fractions to decimals. After completing this tutorial, you will find yourself at a moderate level of expertise in converting fractions to decimals, from where you can advance further.

Prerequisites

Before proceeding with this tutorial, you need a basic knowledge of elementary math concepts such as number sense, addition, subtraction, multiplication, division, whole numbers, fractions, types of fractions, decimals, comparing and ordering whole numbers and so on.

Problem 1

Add 67.07 + 13.41 7.30 6.82

Solution

Step 1:

We first add 67.07 + 13.41 = 80.48

Step 2:

Next we add the two negative decimals 7.30 + 6.82 = 14.12

Step 3:

Now 67.07 + 13.41 7.30 6.82 = 80.48 14.12 = 66.36

Step 4:

So 67.07 + 13.41 7.30 6.82 = 66.36

Problem 2

Add 89.03 + 19.15 8.60 7.92

Solution

Step 1:

We first add 89.03 + 19.15 = 108.18

Step 2:

Next we add the two negative decimals 8.60 + 7.92 = 16.52

Step 3:

Now 89.03 + 19.15 8.60 7.92 = 108.18 16.52 = 91.66

Step 4:

So 89.03 + 19.15 8.60 7.92 = 91.66