Batch Reactor Design Equations

In most batch reactors, the longer a reactant stays in the reactor, the more the reactant is converted to product until either equilibrium is reached or the reactant is exhausted. Consequently, in batch systems the conversion X is a function of the time the reactants spend in the reactor. If N_A0 is the number of moles of A initially present in the reactor (i.e., t = 0), then the total number of moles of A that have reacted (i.e., have been consumed) after a time t is [N_A0X].

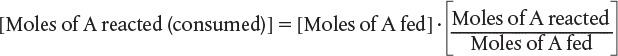
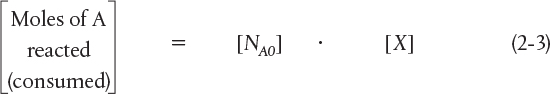
Now, the number of moles of A that remain in the reactor after a time t, N_A, can be expressed in terms of N_A0 and X:

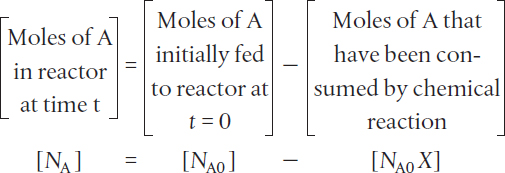
The number of moles of A in the reactor after a conversion X has been achieved is

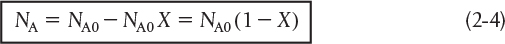
When no spatial variations in reaction rate exist, the mole balance on species A for a batch system is given by the following equation [cf. Equation (1-5)]:

Moles of A in the reactor at a time t

This equation is valid whether or not the reactor volume is constant. In the general reaction, Equation (2-2), reactant A is disappearing; therefore, we multiply both sides of Equation (2-5) by -1 to obtain the mole balance for the batch reactor in the form

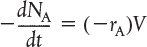
The rate of disappearance of A, −r_A, in this reaction might be given by a rate law similar to Equation (1-2), such as −r_A = kC_AC_B.

For batch reactors, we are interested in determining how long to leave the reactants in the reactor to achieve a certain conversion X. To determine this length of time, we write the mole balance, Equation (2-5), in terms of conversion by differentiating Equation (2-4) with respect to time, remembering that N_A0 is the number of moles of A initially present in the reactor and is therefore a constant with respect to time.

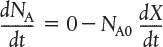
Combining the above with Equation (2-5) yields

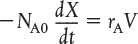
For a batch reactor, the design equation in differential form is

Batch reactor (BR) design equation

We call Equation (2-6) the differential form of the design equation for a batch reactor because we have written the mole balance in terms of conversion. The differential forms of the batch reactor mole balances, Equations (2-5) and (2-6), are often used in the interpretation of reaction rate data (Chapter 7) and for reactors with heat effects (Chapters 11–13), respectively. Batch reactors are frequently used in industry for both gas-phase and liquid-phase reactions. The laboratory bomb calorimeter reactor is widely used for obtaining reaction rate data. Liquid-phase reactions are frequently carried out in batch reactors when small-scale production is desired or operating difficulties rule out the use of continuous-flow systems.

Uses of a BR

To determine the time to achieve a specified conversion X, we first separate the variables in Equation (2-6) as follows:

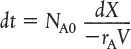
Batch time t to achieve a conversion X

This equation is now integrated with the limits that the reaction begins at time equals zero where there is no conversion initially (when t = 0, X = 0) and ends at time t when a conversion X is achieved (i.e., when t = t, then X = X). Carrying out the integration, we obtain the time t necessary to achieve a conversion X in a batch reactor

The longer the reactants are left in the reactor, the greater the conversion will be. Equation (2-6) is the differential form of the design equation, and Equation (2-7) is the integral form of the design equation for a batch reactor.