Rackett Equation
A useful and accurate method for the calculation of liquid molar volumes at saturation is the Rackett equation. In its modified form, it gives the molar volume of saturated liquid as

where VL is the molar volume at saturation, Tc is the critical temperature, Pc is the critical pressure, Tr = T/Tc is the reduced temperature and ZR is a parameter specific to the fluid. Perry’s Chemical Engineers’ Handbook [2] lists the values for some common fluids10. If ZR is not available, it can be replaced by the compressibility factor at the critical point, Zc = PcVc/RTc, which is usually tabulated. If we use the critical compressibility factor in eq. (2.56), the Rackett equation is simplified and takes the form
10. Table 2-396 in Ref. [2].

where Vc is the critical volume. The Rackett equation is empirical but quite accurate, even in the above simplified form, which contains no adjustable parameters.
Note
Molar Volume of Compressed Liquid
At temperatures well below critical, liquids are practically incompressible and we may assume κ ≈ 0. In this approximation, an isotherm on the PV graph is almost perpendicular to the volume axis. Accordingly, the molar volume of a compressed liquid is essentially the same as that of the saturated liquid at the same temperature. The volume of saturated liquid is often tabulated, or it can be calculated from empirical equations such as the Rackett equation. Therefore, the volume of compressed liquid can be estimated quite accurately from the volume of the saturated liquid at the same temperature. This approximation breaks down close to the critical point where the liquid phase becomes quite compressible.
Example 2.13: Thermal Expansion of Acetone
Perry’s Chemical Engineers’ Handbook provides the following equation for the thermal expansion of liquids (p. 2-131 in Ref. [2]):
V = V0 (1+ a1t + a2t2 + a3t3)
where V0 is the specific volume at 0 °C, V is the volume at temperature t, and t is in °C. For acetone, the values of the parameters a1, a2, a3, are
a1 = 1.3240 × 10−3 a2 = 3.8090 × 10−6 a3 = −0.87983 × 10−8.
Calculate the volumetric coefficient of thermal expansion of acetone at 20 °C and the percent increase in volume upon a temperature increase from 20 °Cto30 °C at constant pressure.
Solution We apply eq. (2.52) to the equation for V given in the problem statement, noting that the derivative must be taken in terms of absolute temperature whereas the equation is given with temperature in °C. Using T = t + 273.15, the required derivative is
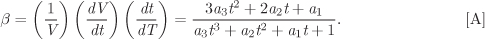
In this equation, t is in °C, and the result is in K−1 or in °C−1 (with respect to temperature differences, as in dT, one degree in the Celsius scale is equal to one kelvin). Using the values of the parameters given in the problem statement at t = 20 °C, we find
β20 °C = 1.426 × 10−3 K−1.
The volume change upon increasing temperature from t1 to t2 is found from eq. (2.54). Keeping pressure constant (dP = 0), integration with respect to temperature gives

The coefficient β is a function of temperature and is given by eq. [A]. A quick approximation is obtained by assuming β to be constant and equal to some average value between t1 and t2. The above integral then becomes
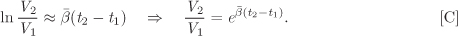
For the average β we will use the simple average between the values at 20 °C and at 30 °C. The coefficient at 30 °C is calculated from eq. [A] and we find β30° C = 1.466 × 10−3 K−1. The mean β is
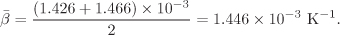
The volume change is calculated from eq. [C] using t2 − t1 = 10 °C= 10 K:
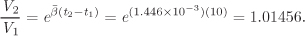
The volume increases by V2/V1 − 1 = 1.45%. If instead of using an average β we perform the integration in eq. [B] using the full form of β from eq. [A], we find V2/V1 = 1.01457. The approximate calculation in this case is essentially the same as the exact result.
Example 2.14: Constant-Volume Heating of Liquid
A glass container is filled with acetone at 25 °C and sealed, leaving no air inside. Determine the pressure that develops in the container when it is heated to 35 °C. The isothermal compressibility of acetone is (see Table 2-188 in Perry’s Chemical Engineers’ Handbook [2]),
κ = 52 × 10−6 bar−1
You may ignore the expansion of the container.
Solution If the expansion of the container is neglected, the volume of the acetone (total, specific, or molar) remains constant. Using dV = 0 in eq. (2.55) we obtain a relationship between temperature and pressure:
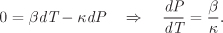
Treating β and κ as constants, integration gives
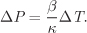
Using the average value of β between temperatures 20 °C and 30 °C, calculated in Example 2.13, and the value for κ given in the problem statement, the pressure increase is
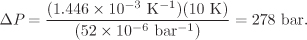
The glass container will most likely break.
Comments This result may seem counterintuitive: if volume increases only by 1.45% when temperature increases by 10 °C, why is it that the pressure generated at fixed volume is so high? This behavior is a consequence of the steepness of the isotherms in the liquid region. Figure 2-14 shows a graph of these isotherms calculated from eq. (2.54) with the values of β and κ for acetone. These lines decrease very steeply, reflecting the fact that volume changes very little with pressure. During constant-volume heating, the state moves along a vertical line from the initial state at 1 bar, 20 °C, to final state at 30 °C. Because isotherms are very steep, pressure increases substantially along a constant-volume path. This behavior is common to all substances that are fairly incompressible. This is, the reason that frozen water pipes burst in winter and water bottles in the freezer break. The physical reason is that molecules in liquids and solids are at close distances from each other, and very close to the point that the intermolecular potential becomes very strongly repulsive (see Figure 1-3). In this region, very small changes to the position of molecules can create enormous repulsion. When we increase temperature, molecules have enough energy for such small changes in position. Normally, the resulting repulsion causes the system to expand but if the volume is constrained, the resulting pressure can be enormous.
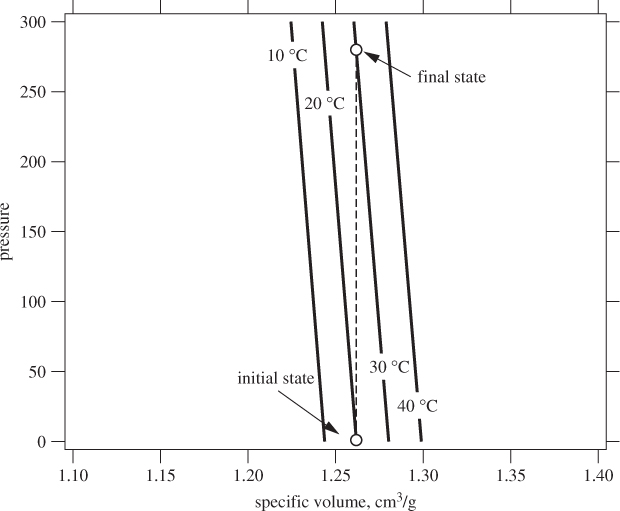
Figure 2-14: Pressure-volume isotherms of acetone (see Example 2.14).
Example 2.15: Rackett Equation
Use the simplified Rackett equation to estimate the density of saturated water at 100 °C.
Solution We collect the following data for water:
Vc = 56 × 10−6 m3/mol, Zc = 0.229, Tc = 647.3K.
At T = 100 °C = 373.15 we have Tr = 0.5765. Using the Rackett equation we find
V = 56 × 10−6 × 0.2290.42350.2857 = 17.67 cm3/mol = 0.9819 cm3/g
from which we obtain the density
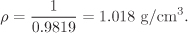
The value from the steam tables is 0.001043 m3/kg = 1.043 cm3/g, a difference of −2.4%.
Example 2.16: Density of Compressed Liquid
Estimate the density of water at 100 °C, 5 bar.
Solution Under the given conditions water is compressed liquid. The pressure is low compared to the critical point; therefore, we may take the volume to be equal to that of saturated liquid at 100 °C. This value is 0.001043 m3/kg.
2.12 Summary
The equation of state is a fundamental property of fluids that describes the relationship between molar volume, temperature, and pressure. This relationship is expressed mathematically as an equation between V, P, and T, or alternatively, between Z, P, and T. The PV graph is a graphical representation of this relationship and a convenient way to present the phase behavior of a pure component. It is a good idea to draw a qualitative PV graph when solving problems involving heating, cooling, compression, or expansion of pure fluids, as a way of becoming oriented in thermodynamic space. Simple processes on this graph is represented by simple paths and help visualize any phase transformations that may occur.
The accurate prediction of the molar volume, or, equivalently, of the compressibility factor, is a requirement in engineering calculations. Several methodologies were discussed in this chapter:
• Tabulated values. Tabulations are available for a large number of pure components. The steam tables is one such example. Usually, however, property tabulations are not as detailed or extensive as the steam tables. Tables are generally the most accurate source for properties. They are not convenient, however, for large-scale calculations.
• Generalized graphs. These graphs are correlations based on corresponding states. Using just three physical constants, critical pressure and temperature, and acentric factor, one can estimate the molar volume of a pure fluid over a very wide range of conditions. This is a very important advantage but it comes with certain limitations. The method is approximate and is based on graphs that have been tweaked to provide overall good accuracy for several different fluids. Necessarily, the agreement will be better for some and worse for others. The method should be used only for normal fluids that are not polar to a significant degree. This covers a large number of compounds but excludes many industrially important molecules, chiefly among them, water.
• Equations of state. An equation of state in mathematical form has the advantage that it can be used in repetitive calculations and is especially suited for computer-based calculations. Industrial software for chemical process design makes extensive use of such equations. The equations discussed in this chapter (van der Waals, Soave-Redlich-Kwong, and Peng-Robinson) incorporate the principle of corresponding states in their constants, which can be computed for any fluid given the critical pressure, critical temperature, and acentric factor. These equations must be used with the same caution as generalized graphs: they should be applied to nonpolar fluids only. The constants of these equations, specifically the part that involves the acentric factor, have been obtained from fitting data for several different fluids to obtain overall good agreement among them. It is possible to modify the constants of an equation of state to improve accuracy for a particular substance, however, the constants given here are specifically for normal fluids.
Of the many equations that were discussed here, two deserve a special note:
Ideal-gas law. The ideal-gas law is the theoretical limit of any equation of state at low pressure. It is a universal limit but its range of applicability is limited to the region we call ideal-gas state. You should resist the temptation to apply the ideal-gas law without justification.
Virial equation. The virial equation has rigorous basis on theory. However, its truncated form, it should be treated as an extrapolation to somewhat higher pressures that those in the ideal-gas state.
• Empirical equations. Empirical equations usually have no basis on theory but give nonetheless very accurate predictions. The Rackett equation is one such example. The limitation is that the range of applicability is typically narrow. The Rackett equation, for example, is only good along the line of saturated liquid.
The availability of several alternative methodologies is a toolbox that facilitates the job of the engineer. It is the responsibility of the engineer to choose the right tool from this toolbox for a given situation.
2.13 Problems
Problem 2.1: a) Use the steam tables to determine the phase of water (liquid or vapor) at following conditions: 25 °C, 1 bar; 80 °C, 10 bar; 120 °C; 50 bar.
b) The vapor pressure of bromobenzene at 40 °C is 10 mm Hg. Determine the phase of bromobenzene at 40 °C, 1 atm.
c) The normal boiling point of fluorobenzene is 84.7 °C. What is the phase of fluorobenzene at 25 °C, 1 atm?
Problem 2.2: Determine the temperature and phase of water from the following information. If the phase is a vapor-liquid mixture, report the fraction of vapor and liquid.
a) The specific volume of water is 100 cm3/g and the pressure 40 bar.
b) The specific volume of water is 100 cm3/g and the pressure 6 bar.
Problem 2.3: Use the steam tables to do the following:
a) A drum 3.5 m3 in volume contains steam at 1 bar, 210 °C. Determine the mass of steam in the drum.
b) Wet steam with quality 15% vapor is to be stored under pressure at 20 bar in a thermally insulated vessel. What is the temperature?
c) If the total mass to be stored is 525 kg, what is the required volume of the vessel?
The conditions are the same as in part (b).
Problem 2.4: A closed tank contains a vapor-liquid mixture of steam at 45 bar with liquid content 25% by mass.
a) Heat is added until the pressure becomes 80 bar. What is the temperature?
b) The pressure is changed until the contents become 100% saturated vapor. What is that pressure?
c) With pressure held constant at 45 bar, steam is added to or removed from the tank, as needed, until the contents are 25% liquid by volume. Calculate the mass of steam that must be added or removed and report it as a percentage of the total mass originally in the tank.
Problem 2.5: The following data are available for a gas:
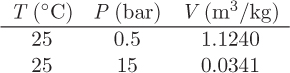
To calculate the molar volume at 25 °C, 12 bar, our team came up with two different suggestions: (a) linear interpolation for V between the given pressure, or (b) linear interpolation for the density ρ = 1/V between the two pressures. Which method do you recommend and why? Under what conditions is your recommendation accurate?
Problem 2.6: A 12 m3 tank contains a liquid/vapor mixture of steam at 15 bar. The volume of the liquid in the tank is 0.5 m3.
a) What is the temperature?
b) What is the total mass in the tank?
c) What is quality of the steam?
d) 87% of the mass in the tank is removed while keeping pressure constant at 15 bar. What is the final temperature in the tank?
Problem 2.7: An eight-liter pressure cooker contains a mixture of steam and liquid water at 2 bar. Through a level indicator we can see that the liquid occupies 25% of the volume inside the cooker.
a) What is the temperature inside the cooker?
b) What is the total mass of water (liquid plus vapor) in the cooker?
c) What is the mass fraction of the liquid?
d) The cooker, while it remains sealed, is placed under running water until its temperature cools to 25 °C. What is the pressure in the cooker?
e) What force does it take to unseal the cooker? The cover is circular with a radius of 20 cm.
Problem 2.8: a) A pressure cooker is filled to the brim with water at 80 °Cand the lid is locked. The temperature is then changed until the contents become saturated liquid. What is the temperature and pressure at that point?
b) A closed pressure cooker contains 50% by volume liquid and 50% water vapor at 1 bar. The pressure is then changed until the point where the contents become a single phase. Is that phase saturated liquid or saturated vapor?
c) A closed rigid vessel that contains a pure fluid is cooled until the contents become saturated vapor. Determine whether the initial state is superheated vapor, compressed liquid, or vapor/liquid.
d) A closed rigid vessel that contains a pure fluid is heated until the contents become saturated liquid. Determine whether the initial state is superheated vapor, compressed liquid, or vapor/liquid.
Problem 2.9: A tank whose volume is 12 m3 contains 6.2 kg of water at 1.4 bar.
a) What is the phase (liquid, vapor, liquid/vapor mixture)?
b) What is the temperature?
c) We add more steam to the tank while maintaining its temperature constant at the value calculated in part b. As a result, the pressure in the tank increases. Determine how much water (in kg) of steam must be added to bring the steam in the tank to the point of condensation.
d) Draw a qualitative PV graph and show the path of the process for part c.
Problem 2.10: a) Use data from the steam tables to construct the PV graph of water. Show the saturated liquid, the saturated vapor, the critical point. Include the isotherms at 100 °C, 200 °C, 300 °C and 400 °C. Make two plots, one using linear axes and one in which the pressure axis is linear but the volume axis is logarithmic.
b) Make a Z − P plot of water using data from the steam tables showing the same information as the PV graph above.
Problem 2.11: Determine whether the truncated virial equation is valid for ethane at the following states:
a) 10 bar, 25 °C.
b) Saturated vapor at 10 bar.
c) 10 bar, −35 °C.
Additional data: The boiling point of ethane at 10 bar is −29 °C.
Problem 2.12: The R&D division of your company has released the following limited data on proprietary compound X-23:

Using this incomplete information estimate as best as you can the following:
a) Phase of X-23 at 12 bar, 25 °C.
b) The molar mass of X-23.
c) The second virial coefficient at 25 °C.
d) The required volume of a tank that is needed to store 20 kg of X-23 at 12 bar, 25 C.
e) State clearly and justify as best as you can all your assumptions and the methods you use.
Problem 2.13: Methane is stored under pressure in a 1 m3 tank. The pressure in the tank is 20 bar and the temperature is 25 °C.
a) Calculate the compressibility factor of methane in the tank from the virial equation truncated after the second term.
b) What is the amount (moles) of methane in the tank?
c) You want to store twice as much methane in the tank at the same temperature. What will be the pressure in the tank?
d) Is it appropriate to use the virial equation for this problem? Explain.
At 25 °C the second virial coefficient of methane is −4.22 × 10−5 m3/mol.
Problem 2.14: Use the truncated virial equation to answer the questions below:
a) A 5 m3 tank contains nitrogen at 110 K, 7 bar. How many kg of nitrogen are in the tank?
b) The tank is cooled until the contents become saturated vapor. What is the pressure and temperature in the tank?
c) Is the use of the truncated virial equation justified in this problem? Additional data: The saturation pressure of nitrogen is given by the following empirical equation:
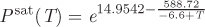
with Psat is in mm Hg and T is in kelvin.
Problem 2.15: a) Calculate the second virial coefficient of water at 200 °C using only data from the steam tables.
b) Use the truncated virial equation along with the second virial coefficient calculated above to estimate the volume of water at 200 °C, 14 bar. How does this value compare with the volume obtained from the steam tables? Discuss this comparison.
Problem 2.16: 1000 kg of methane is to be stored in a tank at 25 °C, 75 bar.
What is the required volume of the tank? (Hint: Use the Pitzer equation with the Lee-Kesler values.)
Problem 2.17: 200 kg of carbon dioxide are stored in a tank at 25 °C and 70 bar.
a) Is carbon dioxide an ideal gas under the conditions in the tank?
b) What is the volume of the tank?
c) How much carbon dioxide must be removed for the pressure of the tank to fall to1bar?
The molecular weight of CO2 is 44 g/mol.
Problem 2.18: A full cylinder of ethylene (C2H4) at 25 °C contains 50 kg of gas at 80 bar.
a) Is ethylene an ideal gas under these conditions? Explain.
b) What is the volume of the cylinder?
c) What is the pressure in the cylinder after 90% of the ethylene has been removed, if temperature is 25 °C?
The molecular weight of ethylene is 28 g/mol.
Problem 2.19: Use the Lee-Kesler method to answer the following: 2000 kg of krypton is to be stored under pressure in a tank at 110 bar, 20 °C. The tank is designed to withstand pressures up to 180 bar.
a) Determine the volume of the tank.
b) Is it safe to store 2500 kg in the tank at 25 °C?
c) Is the Lee-Kesler method appropriate?
Problem 2.20: A tank is divided by a rigid, thermally conducting partition into two equal parts, A and B, each 10 m3 in volume. Part A contains saturated liquid n-butane at 20 °C, 2.07 bar; part B contains saturated n-butane vapor, also at 20 °C, 2.07 bar. Each part is equipped with a safety alarm that will go off if pressure exceeds 40 bar.
a) How many moles of n-butane is in part A of the tank?
b) How many moles of n-butane is in part B of the tank?
c) The tank is heated slowly in such a way that the temperature in both parts rises at the same rate. As soon as the alarm goes off, the heating stops. Which alarm goes off, that of part A or part B?
d) What is the temperature when the alarm sounds?
Additional data: The volume expansivity and the isothermal compressibility of liquid n-butane are given below and may be assumed to be constant:
β = 2.54 × 10−3 K−1, κ = 3.4 × 10−4 bar−1.
Problem 2.21: a) A tank contains 10,000 kg of xenon at 132 °C, 82 bar. The plant supervisor asks you to remove xenon and fill the tank with 10,000 kg of steam at 200 °C. What is the pressure in the tank when it is filled with steam?
b) After the tank has been filled with steam, 5000 kg are withdrawn for use elsewhere in the plant. What is the pressure, if temperature remains at 200 °C?
Problem 2.22: The boiling point of o-xylene at 1 bar is 139 °C.
a) What is the state of o-xylene at 0.1 bar, 200 °C?
b) 100 moles of o-xylene are to be loaded in a tank at 0.1 bar, 200 °C. What is the required volume of the tank?
c) The tank can safely withstand pressures up to 44.9 bar. How much o-xylene can be stored in the tank under maximum pressure at 200 °C?
Problem 2.23: a) Determine the percent change in volume when olive oil is heated at constant pressure from 18 °C to 40 °C.
b) Olive oil is stored in a full container at 18 °C. Determine the pressure that will develop in the container if the temperature in the storage room rises to 40 °C.
Additional data: The volume expansion of olive oil is given by the empirical equation
V = V0(1 + a1t + a2t2 + a3t3)
where t is temperature in °C, V0 is the volume at 0 °C, and the coefficients in the equation are
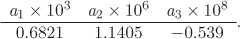
The coefficient of isothermal compression is
κ = 52 × 10−6 bar−1.
(Data from Perry’s Chemical Engineers’ Handbook, 7th ed., Tables 2-147 and 2-188.)
Problem 2.24: A 0.5 m3 tank will be used to store CO2 at 20 °C. Using the SRK equation answer the following:
a) Determine the maximum amount (kg) of CO2 that can be stored safely if the tank can withstand a maximum pressure of 70 bar.
b) Repeat if the maximum pressure is 60 bar.
c) Repeat at 50 bar.
Problem 2.25: Use the SRK equation to answer the following:
a) 5000 kg of isobutane is to be stored in a tank at 60 psi, 70°F. What is the required tank volume?
b) Since the temperature in the summer can get as high as 95°F, determine the pressure that the tank must withstand to avoid rupture.
Problem 2.26: Use the SRK equation to calculate the molar volume of isobutane at the following states:
a) 30 °C, 1 bar.
b) 30 °C, 10 bar.
c) Saturated liquid at 30 °C.
d) Saturated vapor at 30 °C.
For parts c and d, compare with the saturated molar volumes reported in the NIST Web Book.
Additional information: The saturation pressure at 30 °C is 4.05 bar.
Problem 2.27: Use the SRK equation to perform the following calculations for isobutane to make a graph that shows three isotherms, one at 30 °C, one at the critical temperature, and one at 150 °C. Make the axis logarithmic in volume and linear in pressure, and select the range in the two axes so that the graph is not crowded and its important features are seen clearly. Report volume in m3/mol, pressure in bar and temperature in °C. Annotate the graph and label the axes properly.
Problem 2.28: The parameters β and κ of a substance are reported to be functions of pressure and temperature and are given below:
β = 1 /T, κ = 1 /P.
a) Determine the equation of state. Assume that at pressure P0 and temperature T0 the volume is known to be V0. Your final answer then should be in terms of P, V, T, P0, T0 and V0.
b) Is this equation appropriate for liquids?
Problem 2.29: Calculate the coefficient of isothermal compressibility of isobutane as saturated liquid and saturated vapor at 30 °C, Psat = 4.05 bar, using the SRK equation. Report the result in bar−1.
Hint: Recall from calculus that
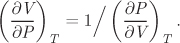
Problem 2.30: Use the steam tables to calculate the value of β of water at the following states:
a) 1 bar, 25 °C.
b) 20 bar, 25 °C.
c) 1 bar, 200 °C.
Problem 2.31: Use the Rackett equation to estimate the volume expansivity of liquid ethanol at 25 °C. State your assumptions clearly.
Leave a Reply