When you can measure what you are speaking about, and express it in numbers, you know something about it. When you cannot measure it, your knowledge is meager and unsatisfactory.
The energy balance is based on the postulate of conservation of energy in the universe. This postulate is known as the first law of thermodynamics. It is a “law” in the same sense as Newton’s laws. It is not refuted by experimental observations within a broadly defined range of conditions, but there is no mathematical proof of its validity. Derived from experimental observation, it quantitatively accounts for energy transformations (heat, work, kinetic, potential). We take the first law as a starting point, a postulate at the macroscopic level, although the conservation of energy in elastic collisions does suggest this inference in the absence of radiation. Facility with computation of energy transformations is a necessary step in developing an understanding of elementary thermodynamics. The first law relates work, heat, and flow to the internal energy, kinetic energy, and potential energy of the system. Therefore, we precede the introduction of the first law with discussion of work and heat.
The energy balance is also known as the first law of thermodynamics.
Chapter Objectives: You Should Be Able to…
1. Explain why enthalpy is a convenient property to define and tabulate.
2. Explain the importance of assuming reversibility in making engineering calculations of work.
3. Calculate work and heat flow for an ideal gas along the following pathways: isothermal, isochoric, adiabatic.
4. Simplify the general energy balance for problems similar to the homework problems, textbook examples, and practice problems.
5. Properly use heat capacity polynomials and latent heats to calculate changes in U, H for ideal gases and condensed phases.
6. Calculate ideal gas or liquid properties relative to an ideal gas or liquid reference state, using the ideal gas law for the vapor phase properties and heats of vaporization.
2.1. Expansion/Contraction Work
There is a simple way that a force on a surface may interact with the system to cause expansion/contraction of the system in volume. This is the type of surface interaction that occurs if we release the latch of a piston, and move the piston in/out while holding the cylinder in a fixed location. Note that a moving boundary is not sufficient to distinguish this type of work—there must be movement of the system boundaries relative to one another. For expansion/contraction interactions, the size of the system must change. This distinction becomes significant when we contrast expansion/contraction work to flow work in Section 2.3.
How can we relate this amount of work to other quantities that are easily measured, like volume and pressure? For a force applied in the x direction, the work done on our system is
dW = Fapplied dx = –Fsystem dx
where we have used Newton’s principle of equal and opposite forces acting on a boundary to relate the applied and system forces. Since it is more convenient to use the system force in calculations, we use the latter form, and drop the subscript with the understanding that we are calculating the work done on the system and basing the calculation on the system force. For a constant force, we may write
W = – FΔx
If F is changing as a function of x then we must use an integral of F,
For a fluid acting on a surface of constant area A, the system force and pressure are related,
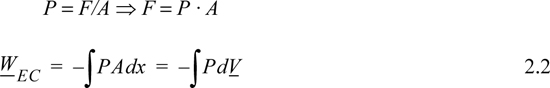
where the subscript EC refers to expansion/contraction work.
In evaluating this expression, a nagging question of perspective comes up. It would be a trivial question except that it causes major headaches when we later try to keep track of positive and negative signs. The question is essentially this: In the discussion above, is positive work being done on the system, or is negative work being done by the system? When we add energy to the system, we consider it a positive input into the system; therefore, putting work into the system should also be considered as a positive input. On the other hand, when a system does work, the energy should go down, and it might be convenient to express work done by the system as positive. The problem is that both perspectives are equally valid—therefore, the choice is arbitrary. Since various textbooks choose differently, there is always confusion about sign conventions. The best we can hope for is to be consistent during our own discussions. We hereby consider work to be positive when performed on the system. Thus, energy put into the system is positive. Because volume decreases when performing work of compression, the sign on the integral for work is negative,
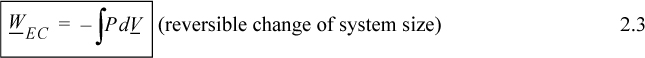
where P and V are of the system. Clarification of “reversible” is given in Section 2.4 on page 42. By comparing Eqn. 2.3 with the definitions of work given by Eqns. 2.1 and 2.2, it should be obvious that the dV term results from expansion/contraction of the boundary of the system. The P results from the force of the system acting at the boundary. Therefore, to use Eqn. 2.3, the pressure in the integral is the pressure of the system at the boundary, and the boundary must move. A system which does not have an expanding/contracting boundary does not have expansion/contraction work.1
Expansion/Contraction work is associated with a change in system size.
2.2. Shaft Work
In a flowing system, we know that a propeller-type device can be used to push a fluid through pipes—this is the basis of a centrifugal pump. Also, a fluid flowing through a similar device could cause movement of a shaft—this is the basis for hydroelectric power generation and the water wheels that powered mills in the early twentieth century. These are the most commonly encountered forms of shaft work in thermodynamics, but there is another slight variation. Suppose an impeller was inserted into a cylinder containing cookie batter and stirred while holding the piston at a fixed volume. We would be putting work into the cylinder, but the system boundaries would neither expand nor contract. All of these cases exemplify shaft work. The essential feature of shaft work is that work is being added or removed without a change in volume of the system. We show in Section 2.8, page 54, that shaft work for a reversible flow process can be computed from
Note that Eqns. 2.3 and 2.4 are distinct and should not be interchanged. Eqn. 2.4 is restricted to shaft work in an open system and Eqn. 2.3 is for expansion/contraction work in a closed system. We later show how selection of the system boundary in a flow system relates the two types of terms on page 54.
Shaft work characterizes the work of a turbine or pump.
2.3. Work Associated with Flow
In engineering applications, most problems involve flowing systems. This means that materials typically flow into a piece of equipment and then flow out of it, crossing well-defined system boundaries in the process. Thus, we need to introduce an additional characterization of work: the work interaction of the system and surroundings when mass crosses a boundary. For example, when a gas is released out of a tank through a valve, the exiting gas pushes the surrounding fluid, doing work on the surroundings. Likewise, when a tank valve is opened to allow gas from a higher pressure source to flow inward, the surroundings do work on the gas already in the system. We calculate the work in these situations most easily by first calculating the rate at which work is done.
Let us first consider a fluid entering a system as shown in Fig. 2.1. We have dW = Fdx, and the work interaction of the system is positive since we are pushing fluid into the system. The rate of work is 
, but 
is velocity, and F = P·A. Further rearranging, recognizing 
, and that the volumetric flow rate may be related to the mass specific volume and the mass flow rate, 
,
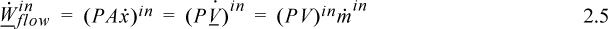
Work associated with fluid flowing in/out of boundaries is called flow work.
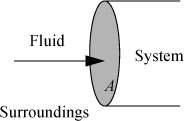
Figure 2.1. Schematic illustration of flow work.
where PV are the properties of the fluid at the point where it crosses the boundary, and 
is the absolute value of the mass flow rate across the boundary. When fluid flows out of the system, work is done on the surroundings and the work interaction of the system is
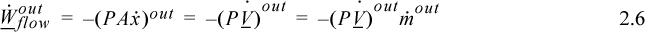
where 
is the absolute value of the mass flow across the boundary, and since work is being done on the surroundings, the work interaction of the system is negative. When flow occurs both in and out, the net flow work is the difference:
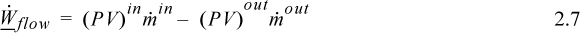
where and are absolute values of the mass flow rates. For more streams, we simply follow the conventions established, and add inlet streams and subtract outlet streams.
2.4. Lost Work versus Reversibility
Real processes involve “lost work.”
In order to properly understand the various characteristic forms that work may assume, we must address an issue which primarily belongs to the upcoming chapter on entropy. The problem is that the generation of disorder reflected by entropy change results in conversion of potentially useful work energy into practically useless thermal energy. If “generation of disorder results in lost work,” then operating in a disorderly fashion results in the lost capability to perform useful work, which we abbreviate by the term: “lost work.” It turns out that the most orderly manner of operating is a hypothetical process known as a reversible process. Typically, this hypothetical, reversible process is applied as an initial approximation of the real process, and then a correction factor is applied to estimate the results for the actual process. It was not mentioned in the discussion of expansion/contraction work, but we implicitly assumed that the process was performed reversibly, so that all of the work on the system was stored in a potentially useful form. To see that this might not always be the case, and how this observation relates to the term “reversible,” consider the problem of stirring cookie batter. Does the cookie batter become unmixed if you stir in the reverse direction? Of course not. The shaft work of stirring has been degraded to effect the randomness of the ingredients. It is impossible to completely recover the work lost in the randomness of this irreversible process. Any real process involves some degree of stirring or mixing, so lost work cannot be eliminated, but we can hope to minimize unnecessary losses if we understand the issue properly.
Consider a process involving gas enclosed in a piston and cylinder. Let the piston be oriented upward so that an expansion of the gas causes the piston to move upward. Suppose that the pressure in the piston is great enough to cause the piston to move upward when the latch is released. How can the process be carried out so that the expansion process yields the maximum work? First, we know that we must eliminate friction to obtain the maximum movement of the piston.
Friction decreases the work available from a process. Frequently we neglect friction to perform a calculation of maximum work.
Leave a Reply