Concepts Demonstrated

Use of the Clapeyron and Antoine equations for vapor pressure correlation and estimation of latent heat of vaporization from the Clapeyron equation.

Numerical Methods Utilized

Linear regressions after proper transformations to a linear expression.

Problem Statement

The Clapeyron equation is commonly used to correlate vapor pressure (P_v) with absolute temperature (T) in °C where ΔH_v is the latent heat of vaporization.

Equation 2-25. 

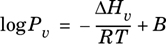
Another common vapor pressure correlation is the Antoine equation, which utilizes three parameters A, B, and C, with P_v typically in mm Hg and T in °C.

Equation 2-26. 

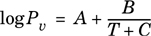
A particular chemical is to be liquefied and stored in gas cylinders in an outside storage shed. The following data were obtained in the laboratory bomb calorimeter measurements. In this calorimeter, the liquid was slowly heated in a sealed container while the temperature and pressure of Table 2-8 were recorded.

Table 2-8. Vapor Pressure Data

T (°C)	17	18	19	21	25	27	28
P(mm Hg)	13.6	22.21	35.54	85.98	413.23	832.62	1160.23

1. Determine the heat vaporization and the constant B using the Clapeyron equation.
2. Assuming the yearly low and hot temperatures in the storage shed are 10°F and 120°F, calculate the expected vapor pressures at these temperature extremes.
3. How do your answers to (b) change when you use the Antoine correlation given by Equation (2-26)?
4. What do you think about storing the cylinders outside?

Solution (Partial)

Finding the heat of vaporization and B in Equation (2-25) requires fitting a straight line to the experimental data. This is accomplished by the regression of log(P_v) versus 1/T, where T is the absolute temperature. This is explained in more detail in Problem 2.5. After the parameters of the regression have been determined, the values of ΔH_v and B can be calculated.

The Antoine equation must first be linearized. This is accomplished by multiplication of both sides of Equation (2-26) by T + C, yielding

Equation 2-27. 

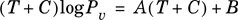
Equation (2-27) can be rearranged:

Equation 2-28. 

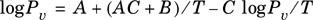
Evaluation of the parameters of Equation (2-27) can be accomplished by defining one new dependent and two new independent variables (columns) given by

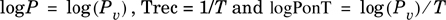
Linear regression with Trec and logPonT as independent and logP as dependent variables will yield the desired parameters.

The linearization of the Antoine equation, in the form of Equation (2-28), is somewhat problematic, in a statistical sense, since the original dependent variable P_v appears in both sides of the equation. However, this linearization usually yields acceptable results. Nonlinear regression will be used in Problem 3.1 to calculate the Antoine equation parameters, and this is the preferred approach in a statistical sense.

Once the constants of the Clapeyron and Antoine equations have been found, the equations can be used to calculate the vapor pressure at different temperatures.

Gas Volume Calculations using Various Equations of State

Concepts Demonstrated

Gas volume calculations using the ideal gas, van der Waals, Soave-Redlich-Kwong, Peng-Robinson, and Beattie-Bridgeman equations of state.

Numerical Methods Utilized

Solution of a single nonlinear algebraic equation.

Problem Statement

It is proposed to use a steel tank to store carbon dioxide at 300 K. The tank is 2.5 m³ in volume, and the maximum pressure it can safely withstand is 100 atm.