Unit Fraction Edge Lengths

Introduction

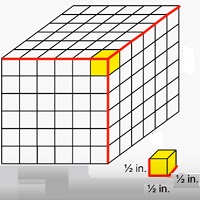
Here we find volume of solids made of cubes with unit fraction edge lengths. Consider for example a solid of dimensions 3 in × 3 in × 3 made of small cubes with 12 inch edge lengths.

In that case the solid is made up of 6 × 6 × 6 small cubes of 12 inch edge lengths. So the volume of the solid in this case would be

Volume = l w h = 6×12×6×12×6×12

= 3 × 3 × 3 = 27 cubic inches

Formula for the volume of solid made of cubes with unit fractional edge lengths

Assuming the solid to be a cube of edge a units

b = number of cubes with unit fractional edge length along each edge

k = unit fractional edge length

Volume of solid = b × k × b × k × b × k cubic units

Example 1

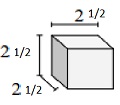
Find the volume of following solid of cubes with unit fraction edge lengths. Each prisms unit is measured in cm (not to scale)

Solution

Step 1:

Solid of cubes with unit fraction edge lengths of 12 cm

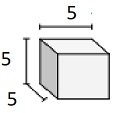
Step 2:

Volume V = l w h = 212×212×212

= 5×12×5×12×5×12

= 1558 cu cm

Example 2

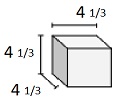
Find the volume of following solid of cubes with unit fraction edge lengths. Each prisms unit is measured in cm (not to scale)

Solution

Step 1:

Solid of cubes with unit fraction edge lengths of 13 cm

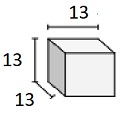
Step 2:

Volume V = l w h = 413×413×413

= 13×13×13×13×13×13

= 811027 cu cm