SECANT METHOD

In Chapter 4, methods for approximating the derivative of a function using finite differences are presented. The secant method uses the idea of finite differences to approximate the derivative in the Newton method formula. Starting with two initial guesses x⁰ and x¹, which need not bracket the root of interest, the approximation to f΄(x) can be written as follows:

Or, in general, after k steps or iterations,

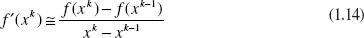
Substituting this approximation into the Newton formula (Equation 1.9), the following iteration formula results for the secant method:

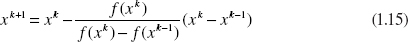
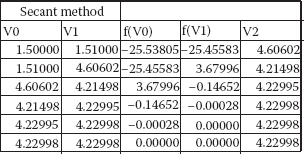
Example 1.5: The Secant Method for van der Waals Equation

The following shows the van der Waals example solved using the secant method. The two initial guesses for V are 1.50 and 1.51—the second was chosen arbitrarily close to the first one. Note that the rate of convergence is about the same as that of Newton’s method. Beware that the secant method is subject to the same potential shortcomings of Newton’s method.