Blog

Data Types

MATLAB does not require any type declaration or dimension statements. Whenever MATLAB encounters a new variable name, it creates the variable and allocates appropriate memory space.

If the variable already exists, then MATLAB replaces the original content with new content and allocates new storage space, where necessary.

For example,

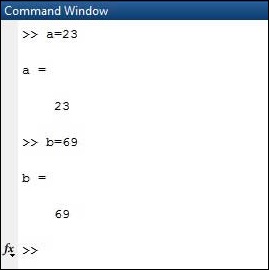
Total = 42

The above statement creates a 1-by-1 matrix named ‘Total’ and stores the value 42 in it.

Data Types Available in MATLAB

MATLAB provides 15 fundamental data types. Every data type stores data that is in the form of a matrix or array. The size of this matrix or array is a minimum of 0-by-0 and this can grow up to a matrix or array of any size.

The following table shows the most commonly used data types in MATLAB −

Sr.No.	Data Type & Description
1	int88-bit signed integer
2	uint88-bit unsigned integer
3	int1616-bit signed integer
4	uint1616-bit unsigned integer
5	int3232-bit signed integer
6	uint3232-bit unsigned integer
7	int6464-bit signed integer
8	uint6464-bit unsigned integer
9	singlesingle precision numerical data
10	doubledouble precision numerical data
11	logicallogical values of 1 or 0, represent true and false respectively
12	charcharacter data (strings are stored as vector of characters)
13	cell arrayarray of indexed cells, each capable of storing an array of a different dimension and data type
14	structureC-like structures, each structure having named fields capable of storing an array of a different dimension and data type
15	function handlepointer to a function
16	user classesobjects constructed from a user-defined class
17	java classesobjects constructed from a Java class

Example

Create a script file with the following code −

str = 'Hello World!'
n = 2345
d = double(n)
un = uint32(789.50)
rn = 5678.92347
c = int32(rn)

When the above code is compiled and executed, it produces the following result −

str = Hello World!
n =  2345
d =  2345
un = 790
rn = 5678.9
c =  5679

Data Type Conversion

MATLAB provides various functions for converting, a value from one data type to another. The following table shows the data type conversion functions −

Function	Purpose
char	Convert to character array (string)
int2str	Convert integer data to string
mat2str	Convert matrix to string
num2str	Convert number to string
str2double	Convert string to double-precision value
str2num	Convert string to number
native2unicode	Convert numeric bytes to Unicode characters
unicode2native	Convert Unicode characters to numeric bytes
base2dec	Convert base N number string to decimal number
bin2dec	Convert binary number string to decimal number
dec2base	Convert decimal to base N number in string
dec2bin	Convert decimal to binary number in string
dec2hex	Convert decimal to hexadecimal number in string
hex2dec	Convert hexadecimal number string to decimal number
hex2num	Convert hexadecimal number string to double-precision number
num2hex	Convert singles and doubles to IEEE hexadecimal strings
cell2mat	Convert cell array to numeric array
cell2struct	Convert cell array to structure array
cellstr	Create cell array of strings from character array
mat2cell	Convert array to cell array with potentially different sized cells
num2cell	Convert array to cell array with consistently sized cells
struct2cell	Convert structure to cell array

Determination of Data Types

MATLAB provides various functions for identifying data type of a variable.

Following table provides the functions for determining the data type of a variable −

Function	Purpose
is	Detect state
isa	Determine if input is object of specified class
iscell	Determine whether input is cell array
iscellstr	Determine whether input is cell array of strings
ischar	Determine whether item is character array
isfield	Determine whether input is structure array field
isfloat	Determine if input is floating-point array
ishghandle	True for Handle Graphics object handles
isinteger	Determine if input is integer array
isjava	Determine if input is Java object
islogical	Determine if input is logical array
isnumeric	Determine if input is numeric array
isobject	Determine if input is MATLAB object
isreal	Check if input is real array
isscalar	Determine whether input is scalar
isstr	Determine whether input is character array
isstruct	Determine whether input is structure array
isvector	Determine whether input is vector
class	Determine class of object
validateattributes	Check validity of array
whos	List variables in workspace, with sizes and types

Example

Create a script file with the following code −

x = 3
isinteger(x)
isfloat(x)
isvector(x)
isscalar(x)
isnumeric(x)
 
x = 23.54
isinteger(x)
isfloat(x)
isvector(x)
isscalar(x)
isnumeric(x)
 
x = [1 2 3]
isinteger(x)
isfloat(x)
isvector(x)
isscalar(x)
 
x = 'Hello'
isinteger(x)
isfloat(x)
isvector(x)
isscalar(x)
isnumeric(x)

When you run the file, it produces the following result −

x = 3
ans = 0
ans = 1
ans = 1
ans = 1
ans = 1
x = 23.540
ans = 0
ans = 1
ans = 1
ans = 1
ans = 1
x =

      1          2          3
ans = 0
ans = 1
ans = 1
ans = 0
x = Hello
ans = 0
ans = 0
ans = 1
ans = 0
ans = 0

May 28, 2024

M-Files
So far, we have used MATLAB environment as a calculator. However, MATLAB is also a powerful programming language, as well as an interactive computational environment.

In previous chapters, you have learned how to enter commands from the MATLAB command prompt. MATLAB also allows you to write series of commands into a file and execute the file as complete unit, like writing a function and calling it.

The M Files

MATLAB allows writing two kinds of program files −
- Scripts − script files are program files with .m extension. In these files, you write series of commands, which you want to execute together. Scripts do not accept inputs and do not return any outputs. They operate on data in the workspace.
- Functions − functions files are also program files with .m extension. Functions can accept inputs and return outputs. Internal variables are local to the function.
You can use the MATLAB editor or any other text editor to create your .mfiles. In this section, we will discuss the script files. A script file contains multiple sequential lines of MATLAB commands and function calls. You can run a script by typing its name at the command line.

Creating and Running Script File

To create scripts files, you need to use a text editor. You can open the MATLAB editor in two ways −
- Using the command prompt
- Using the IDE
If you are using the command prompt, type edit in the command prompt. This will open the editor. You can directly type edit and then the filename (with .m extension)
```
edit 
Or
edit <filename>
```
The above command will create the file in default MATLAB directory. If you want to store all program files in a specific folder, then you will have to provide the entire path.

Let us create a folder named progs. Type the following commands at the command prompt (>>) −
```
mkdir progs    % create directory progs under default directory
chdir progs    % changing the current directory to progs
edit  prog1.m  % creating an m file named prog1.m
```
If you are creating the file for first time, MATLAB prompts you to confirm it. Click Yes.

Alternatively, if you are using the IDE, choose NEW -> Script. This also opens the editor and creates a file named Untitled. You can name and save the file after typing the code.

Type the following code in the editor −
```
NoOfStudents = 6000;
TeachingStaff = 150;
NonTeachingStaff = 20;

Total = NoOfStudents + TeachingStaff ...
   + NonTeachingStaff;
disp(Total);
```
After creating and saving the file, you can run it in two ways −
- Clicking the Run button on the editor window or
- Just typing the filename (without extension) in the command prompt: >> prog1
The command window prompt displays the result −
6170
Example

Create a script file, and type the following code −
```
a = 5; b = 7;
c = a + b
d = c + sin(b)
e = 5 * d
f = exp(-d)
```
When the above code is compiled and executed, it produces the following result −
```
c =  12
d =  12.657
e =  63.285
f =    3.1852e-06
```
May 28, 2024

Commands

MATLAB is an interactive program for numerical computation and data visualization. You can enter a command by typing it at the MATLAB prompt ‘>>’ on the Command Window.

In this section, we will provide lists of commonly used general MATLAB commands.

Commands for Managing a Session

MATLAB provides various commands for managing a session. The following table provides all such commands −

Command	Purpose
clc	Clears command window.
clear	Removes variables from memory.
exist	Checks for existence of file or variable.
global	Declares variables to be global.
help	Searches for a help topic.
lookfor	Searches help entries for a keyword.
quit	Stops MATLAB.
who	Lists current variables.
whos	Lists current variables (long display).

Commands for Working with the System

MATLAB provides various useful commands for working with the system, like saving the current work in the workspace as a file and loading the file later.

It also provides various commands for other system-related activities like, displaying date, listing files in the directory, displaying current directory, etc.

The following table displays some commonly used system-related commands −

Command	Purpose
cd	Changes current directory.
date	Displays current date.
delete	Deletes a file.
diary	Switches on/off diary file recording.
dir	Lists all files in current directory.
load	Loads workspace variables from a file.
path	Displays search path.
pwd	Displays current directory.
save	Saves workspace variables in a file.
type	Displays contents of a file.
what	Lists all MATLAB files in the current directory.
wklread	Reads .wk1 spreadsheet file.

Input and Output Commands

MATLAB provides the following input and output related commands −

Command	Purpose
disp	Displays contents of an array or string.
fscanf	Read formatted data from a file.
format	Controls screen-display format.
fprintf	Performs formatted writes to screen or file.
input	Displays prompts and waits for input.
;	Suppresses screen printing.

The fscanf and fprintf commands behave like C scanf and printf functions. They support the following format codes −

Format Code	Purpose
%s	Format as a string.
%d	Format as an integer.
%f	Format as a floating point value.
%e	Format as a floating point value in scientific notation.
%g	Format in the most compact form: %f or %e.
\n	Insert a new line in the output string.
\t	Insert a tab in the output string.

The format function has the following forms used for numeric display −

Format Function	Display up to
format short	Four decimal digits (default).
format long	16 decimal digits.
format short e	Five digits plus exponent.
format long e	16 digits plus exponents.
format bank	Two decimal digits.
format +	Positive, negative, or zero.
format rat	Rational approximation.
format compact	Suppresses some line feeds.
format loose	Resets to less compact display mode.

Vector, Matrix and Array Commands

The following table shows various commands used for working with arrays, matrices and vectors −

Command	Purpose
cat	Concatenates arrays.
find	Finds indices of nonzero elements.
length	Computes number of elements.
linspace	Creates regularly spaced vector.
logspace	Creates logarithmically spaced vector.
max	Returns largest element.
min	Returns smallest element.
prod	Product of each column.
reshape	Changes size.
size	Computes array size.
sort	Sorts each column.
sum	Sums each column.
eye	Creates an identity matrix.
ones	Creates an array of ones.
zeros	Creates an array of zeros.
cross	Computes matrix cross products.
dot	Computes matrix dot products.
det	Computes determinant of an array.
inv	Computes inverse of a matrix.
pinv	Computes pseudoinverse of a matrix.
rank	Computes rank of a matrix.
rref	Computes reduced row echelon form.
cell	Creates cell array.
celldisp	Displays cell array.
cellplot	Displays graphical representation of cell array.
num2cell	Converts numeric array to cell array.
deal	Matches input and output lists.
iscell	Identifies cell array.

Plotting Commands

MATLAB provides numerous commands for plotting graphs. The following table shows some of the commonly used commands for plotting −

Command	Purpose
axis	Sets axis limits.
fplot	Intelligent plotting of functions.
grid	Displays gridlines.
plot	Generates xy plot.
print	Prints plot or saves plot to a file.
title	Puts text at top of plot.
xlabel	Adds text label to x-axis.
ylabel	Adds text label to y-axis.
axes	Creates axes objects.
close	Closes the current plot.
close all	Closes all plots.
figure	Opens a new figure window.
gtext	Enables label placement by mouse.
hold	Freezes current plot.
legend	Legend placement by mouse.
refresh	Redraws current figure window.
set	Specifies properties of objects such as axes.
subplot	Creates plots in subwindows.
text	Places string in figure.
bar	Creates bar chart.
loglog	Creates log-log plot.
polar	Creates polar plot.
semilogx	Creates semilog plot. (logarithmic abscissa).
semilogy	Creates semilog plot. (logarithmic ordinate).
stairs	Creates stairs plot.
stem	Creates stem plot.

May 28, 2024

Variables
In MATLAB environment, every variable is an array or matrix.

You can assign variables in a simple way. For example,
```
x = 3	       % defining x and initializing it with a value
```
MATLAB will execute the above statement and return the following result −
```
x = 3
```
It creates a 1-by-1 matrix named x and stores the value 3 in its element. Let us check another example,
```
x = sqrt(16) 	% defining x and initializing it with an expression
```
MATLAB will execute the above statement and return the following result −
```
x = 4
```
Please note that −
- Once a variable is entered into the system, you can refer to it later.
- Variables must have values before they are used.
- When an expression returns a result that is not assigned to any variable, the system assigns it to a variable named ans, which can be used later.
For example,
```
sqrt(78)
```
MATLAB will execute the above statement and return the following result −
```
ans =  8.8318
```
You can use this variable ans −
```
sqrt(78);
9876/ans
```
MATLAB will execute the above statement and return the following result −
```
ans =  1118.2
```
Let’s look at another example −
x = 7 * 8; y = x * 7.89
MATLAB will execute the above statement and return the following result −
```
y =  441.84
```
Multiple Assignments

You can have multiple assignments on the same line. For example,
```
a = 2; b = 7; c = a * b
```
MATLAB will execute the above statement and return the following result −
```
c = 14
```
I have forgotten the Variables!

The who command displays all the variable names you have used.
```
who
```
MATLAB will execute the above statement and return the following result −
```
Your variables are:
a    ans  b    c   
```
The whos command displays little more about the variables −
- Variables currently in memory
- Type of each variables
- Memory allocated to each variable
- Whether they are complex variables or not
```
whos
```
MATLAB will execute the above statement and return the following result −
```
Attr Name        Size        Bytes      Class
==== ====        ====        ====       ===== 
   a             1x1           8        double
   ans           1x70         757        cell
   b             1x1           8        double
   c             1x1           8        double

Total is 73 elements using 781 bytes     
```
The clear command deletes all (or the specified) variable(s) from the memory.
```
clear x     % it will delete x, won't display anything
clear       % it will delete all variables in the workspace
        %  peacefully and unobtrusively 
```
Long Assignments

Long assignments can be extended to another line by using an ellipses (…). For example,
```
initial_velocity = 0;
acceleration = 9.8;
time = 20;
final_velocity = initial_velocity + acceleration * time
```
MATLAB will execute the above statement and return the following result −
final_velocity = 196
The format Command

By default, MATLAB displays numbers with four decimal place values. This is known as short format.

However, if you want more precision, you need to use the format command.

The format long command displays 16 digits after decimal.

For example −
```
format long
x = 7 + 10/3 + 5 ^ 1.2
```
MATLAB will execute the above statement and return the following result−
```
x = 17.2319816406394
```
Another example,
```
format short
x = 7 + 10/3 + 5 ^ 1.2
```
MATLAB will execute the above statement and return the following result −
```
x = 17.232
```
The format bank command rounds numbers to two decimal places. For example,
```
format bank
daily_wage = 177.45;
weekly_wage = daily_wage * 6
```
MATLAB will execute the above statement and return the following result −
```
weekly_wage = 1064.70
```
MATLAB displays large numbers using exponential notation.

The format short e command allows displaying in exponential form with four decimal places plus the exponent.

For example,
```
format short e
4.678 * 4.9
```
MATLAB will execute the above statement and return the following result −
ans = 2.2922e+01
The format long e command allows displaying in exponential form with four decimal places plus the exponent. For example,
```
format long e
x = pi
```
MATLAB will execute the above statement and return the following result −
```
x = 3.141592653589793e+00
```
The format rat command gives the closest rational expression resulting from a calculation. For example,
```
format rat
4.678 * 4.9
```
MATLAB will execute the above statement and return the following result −
```
ans = 34177/1491 
```
Creating Vectors

A vector is a one-dimensional array of numbers. MATLAB allows creating two types of vectors −
- Row vectors
- Column vectors
Row vectors are created by enclosing the set of elements in square brackets, using space or comma to delimit the elements.

For example,
```
r = [7 8 9 10 11]
```
MATLAB will execute the above statement and return the following result −
```
r =

   7    8    9   10   11 
```
Another example,
```
r = [7 8 9 10 11];
t = [2, 3, 4, 5, 6];
res = r + t
```
MATLAB will execute the above statement and return the following result −
```
res =

     9         11         13         15         17
```
Column vectors are created by enclosing the set of elements in square brackets, using semicolon(;) to delimit the elements.
```
c = [7;  8;  9;  10; 11]
```
MATLAB will execute the above statement and return the following result −
```
c =
   7       
   8       
   9       
  10       
  11  
```
Creating Matrices

A matrix is a two-dimensional array of numbers.

In MATLAB, a matrix is created by entering each row as a sequence of space or comma separated elements, and end of a row is demarcated by a semicolon. For example, let us create a 3-by-3 matrix as −
```
m = [1 2 3; 4 5 6; 7 8 9]
```
MATLAB will execute the above statement and return the following result −
```
m =
   1              2              3       
   4              5              6       
   7              8              9       </code></pre>
```
May 28, 2024


		
		
			
			Basic Syntax
			
MATLAB environment behaves like a super-complex calculator. You can enter commands at the >> command prompt.



MATLAB is an interpreted environment. In other words, you give a command and MATLAB executes it right away.



Hands on Practice



Type a valid expression, for example,



5 + 5



And press ENTER



When you click the Execute button, or type Ctrl+E, MATLAB executes it immediately and the result returned is −



ans = 10




Let us take up few more examples −



3 ^ 2	       % 3 raised to the power of 2



When you click the Execute button, or type Ctrl+E, MATLAB executes it immediately and the result returned is −



ans = 9




Another example,



sin(pi /2)	  % sine of angle 90^o




When you click the Execute button, or type Ctrl+E, MATLAB executes it immediately and the result returned is −



ans = 1




Another example,



7/0		      % Divide by zero



When you click the Execute button, or type Ctrl+E, MATLAB executes it immediately and the result returned is −



ans = Inf
warning: division by zero




Another example,



732 * 20.3	



When you click the Execute button, or type Ctrl+E, MATLAB executes it immediately and the result returned is −



ans =  1.4860e+04




MATLAB provides some special expressions for some mathematical symbols, like pi for π, Inf for ∞, i (and j) for √-1 etc. Nan stands for ‘not a number’.



Use of Semicolon (;) in MATLAB



Semicolon (;) indicates end of statement. However, if you want to suppress and hide the MATLAB output for an expression, add a semicolon after the expression.



For example,



x = 3;
y = x + 5



When you click the Execute button, or type Ctrl+E, MATLAB executes it immediately and the result returned is −



y =  8




Adding Comments



The percent symbol (%) is used for indicating a comment line. For example,



x = 9	     % assign the value 9 to x



You can also write a block of comments using the block comment operators % { and % }.



The MATLAB editor includes tools and context menu items to help you add, remove, or change the format of comments.



Commonly used Operators and Special Characters



MATLAB supports the following commonly used operators and special characters −



Operator Purpose
+ Plus; addition operator.
– Minus; subtraction operator.
* Scalar and matrix multiplication operator.
.* Array multiplication operator.
^ Scalar and matrix exponentiation operator.
.^ Array exponentiation operator.
\ Left-division operator.
/ Right-division operator.
.\ Array left-division operator.
./ Array right-division operator.
: Colon; generates regularly spaced elements and represents an entire row or column.
( ) Parentheses; encloses function arguments and array indices; overrides precedence.
[ ] Brackets; enclosures array elements.
. Decimal point.
… Ellipsis; line-continuation operator
, Comma; separates statements and elements in a row
; Semicolon; separates columns and suppresses display.
% Percent sign; designates a comment and specifies formatting.
_ Quote sign and transpose operator.
._ Nonconjugated transpose operator.
= Assignment operator.



Special Variables and Constants



MATLAB supports the following special variables and constants −



Name Meaning
ans Most recent answer.
eps Accuracy of floating-point precision.
i,j The imaginary unit √-1.
Inf Infinity.
NaN Undefined numerical result (not a number).
pi The number π



Naming Variables



Variable names consist of a letter followed by any number of letters, digits or underscore.



MATLAB is case-sensitive.



Variable names can be of any length, however, MATLAB uses only first N characters, where N is given by the function namelengthmax.



Saving Your Work



The save command is used for saving all the variables in the workspace, as a file with .mat extension, in the current directory.



For example,





save myfile






You can reload the file anytime later using the load command.



load myfile


			May 28, 2024

Environment Setup Local Environment Setup Setting up MATLAB environment is a matter of few clicks. The installer can be downloaded from here. MathWorks provides the licensed product, a trial version and a student version as well. You need to log into the site and wait a little for their approval. After downloading the installer the software can be installed through few clicks. Understanding the MATLAB Environment MATLAB development IDE can be launched from the icon created on the desktop. The main working window in MATLAB is called the desktop. When MATLAB is started, the desktop appears in its default layout − The desktop has the following panels − Current Folder − This panel allows you to access the project folders and files. Command Window − This is the main area where commands can be entered at the command line. It is indicated by the command prompt (>>). Workspace − The workspace shows all the variables created and/or imported from files. Command History − This panel shows or return commands that are entered at the command line. Set up GNU Octave If you are willing to use Octave on your machine ( Linux, BSD, OS X or Windows ), then kindly download latest version from Download GNU Octave. You can check the given installation instructions for your machine. May 28, 2024
Overview MATLAB (matrix laboratory) is a fourth-generation high-level programming language and interactive environment for numerical computation, visualization and programming. MATLAB is developed by MathWorks. It allows matrix manipulations; plotting of functions and data; implementation of algorithms; creation of user interfaces; interfacing with programs written in other languages, including C, C++, Java, and FORTRAN; analyze data; develop algorithms; and create models and applications. It has numerous built-in commands and math functions that help you in mathematical calculations, generating plots, and performing numerical methods. MATLAB’s Power of Computational Mathematics MATLAB is used in every facet of computational mathematics. Following are some commonly used mathematical calculations where it is used most commonly − Dealing with Matrices and Arrays 2-D and 3-D Plotting and graphics Linear Algebra Algebraic Equations Non-linear Functions Statistics Data Analysis Calculus and Differential Equations Numerical Calculations Integration Transforms Curve Fitting Various other special functions Features of MATLAB Following are the basic features of MATLAB − It is a high-level language for numerical computation, visualization and application development. It also provides an interactive environment for iterative exploration, design and problem solving. It provides vast library of mathematical functions for linear algebra, statistics, Fourier analysis, filtering, optimization, numerical integration and solving ordinary differential equations. It provides built-in graphics for visualizing data and tools for creating custom plots. MATLAB’s programming interface gives development tools for improving code quality maintainability and maximizing performance. It provides tools for building applications with custom graphical interfaces. It provides functions for integrating MATLAB based algorithms with external applications and languages such as C, Java, .NET and Microsoft Excel. Uses of MATLAB MATLAB is widely used as a computational tool in science and engineering encompassing the fields of physics, chemistry, math and all engineering streams. It is used in a range of applications including − Signal Processing and Communications Image and Video Processing Control Systems Test and Measurement Computational Finance Computational Biology May 28, 2024

Operator	Purpose
+	Plus; addition operator.
–	Minus; subtraction operator.
*	Scalar and matrix multiplication operator.
.*	Array multiplication operator.
^	Scalar and matrix exponentiation operator.
.^	Array exponentiation operator.
\	Left-division operator.
/	Right-division operator.
.\	Array left-division operator.
./	Array right-division operator.
:	Colon; generates regularly spaced elements and represents an entire row or column.
( )	Parentheses; encloses function arguments and array indices; overrides precedence.
[ ]	Brackets; enclosures array elements.
.	Decimal point.
…	Ellipsis; line-continuation operator
,	Comma; separates statements and elements in a row
;	Semicolon; separates columns and suppresses display.
%	Percent sign; designates a comment and specifies formatting.
_	Quote sign and transpose operator.
._	Nonconjugated transpose operator.
=	Assignment operator.

Name	Meaning
ans	Most recent answer.
eps	Accuracy of floating-point precision.
i,j	The imaginary unit √-1.
Inf	Infinity.
NaN	Undefined numerical result (not a number).
pi	The number π


		
		
			
			Error Handling
			
Go programming provides a pretty simple error handling framework with inbuilt error interface type of the following declaration −



type error interface {
   Error() string
}




Functions normally return error as last return value. Use errors.New to construct a basic error message as following −



func Sqrt(value float64)(float64, error) {
   if(value < 0){
  return 0, errors.New("Math: negative number passed to Sqrt")   }
   return math.Sqrt(value), nil
}



Use return value and error message.



result, err:= Sqrt(-1)

if err != nil {
   fmt.Println(err)
}



Example



Live Demo



package main

import "errors"
import "fmt"
import "math"

func Sqrt(value float64)(float64, error) {
   if(value < 0){
  return 0, errors.New("Math: negative number passed to Sqrt")   }
   return math.Sqrt(value), nil
}
func main() {
   result, err:= Sqrt(-1)

   if err != nil {
  fmt.Println(err)   } else {
  fmt.Println(result)   }
   
   result, err = Sqrt(9)

   if err != nil {
  fmt.Println(err)   } else {
  fmt.Println(result)   }
}



When the above code is compiled and executed, it produces the following result −



Math: negative number passed to Sqrt
3


			May 28, 2024


		
		
			
			Interfaces
			
Go programming provides another data type called interfaces which represents a set of method signatures. The struct data type implements these interfaces to have method definitions for the method signature of the interfaces.



Syntax



/* define an interface */
type interface_name interface {
   method_name1 [return_type]
   method_name2 [return_type]
   method_name3 [return_type]
   ...
   method_namen [return_type]
}

/* define a struct */
type struct_name struct {
   /* variables */
}

/* implement interface methods*/
func (struct_name_variable struct_name) method_name1() [return_type] {
   /* method implementation */
}
...
func (struct_name_variable struct_name) method_namen() [return_type] {
   /* method implementation */
}




Example



Live Demo



package main

import ("fmt" "math")

/* define an interface */
type Shape interface {
   area() float64
}

/* define a circle */
type Circle struct {
   x,y,radius float64
}

/* define a rectangle */
type Rectangle struct {
   width, height float64
}

/* define a method for circle (implementation of Shape.area())*/
func(circle Circle) area() float64 {
   return math.Pi * circle.radius * circle.radius
}

/* define a method for rectangle (implementation of Shape.area())*/
func(rect Rectangle) area() float64 {
   return rect.width * rect.height
}

/* define a method for shape */
func getArea(shape Shape) float64 {
   return shape.area()
}

func main() {
   circle := Circle{x:0,y:0,radius:5}
   rectangle := Rectangle {width:10, height:5}
   
   fmt.Printf("Circle area: %f\n",getArea(circle))
   fmt.Printf("Rectangle area: %f\n",getArea(rectangle))
}



When the above code is compiled and executed, it produces the following result −



Circle area: 78.539816
Rectangle area: 50.000000


			May 28, 2024

Recursion Recursion is the process of repeating items in a self-similar way. The same concept applies in programming languages as well. If a program allows to call a function inside the same function, then it is called a recursive function call. Take a look at the following example − func recursion() { recursion() /* function calls itself */ } func main() { recursion() } The Go programming language supports recursion. That is, it allows a function to call itself. But while using recursion, programmers need to be careful to define an exit condition from the function, otherwise it will go on to become an infinite loop. Examples of Recursion in Go Recursive functions are very useful to solve many mathematical problems such as calculating factorial of a number, generating a Fibonacci series, etc. Example 1: Calculating Factorial Using Recursion in Go The following example calculates the factorial of a given number using a recursive function − package main import "fmt" func factorial(i int)int { if(i <= 1) { return 1 } return i * factorial(i - 1) } func main() { var i int = 15 fmt.Printf("Factorial of %d is %d", i, factorial(i)) } When the above code is compiled and executed, it produces the following result − Factorial of 15 is 1307674368000 Example 2: Fibonacci Series Using Recursion in Go The following example shows how to generate a Fibonacci series of a given number using a recursive function package main import "fmt" func fibonaci(i int) (ret int) { if i == 0 { return 0 } if i == 1 { return 1 } return fibonaci(i-1) + fibonaci(i-2) } func main() { var i int for i = 0; i < 10; i++ { fmt.Printf("%d ", fibonaci(i)) } } When the above code is compiled and executed, it produces the following result − 0 1 1 2 3 5 8 13 21 34 May 28, 2024


	
	
		
	
	
	
	
		
			←Previous Page
			1
…
160
161
162
163
164
…
199
			Next Page→

Blog

Data Types Available in MATLAB

Example

Data Type Conversion

Determination of Data Types

Example

The M Files

Creating and Running Script File

Example

Commands for Managing a Session

Commands for Working with the System

Input and Output Commands

Vector, Matrix and Array Commands

Plotting Commands

Multiple Assignments

I have forgotten the Variables!

Long Assignments

The format Command

Creating Vectors

Creating Matrices

Hands on Practice

Use of Semicolon (;) in MATLAB

Adding Comments

Commonly used Operators and Special Characters

Special Variables and Constants

Naming Variables

Saving Your Work

Local Environment Setup

Understanding the MATLAB Environment

Set up GNU Octave

MATLAB’s Power of Computational Mathematics

Features of MATLAB

Uses of MATLAB

Example

Syntax

Example

Examples of Recursion in Go

Example 1: Calculating Factorial Using Recursion in Go

Example 2: Fibonacci Series Using Recursion in Go