Educational

Blog

  • Functions

    A function is a group of statements that together perform a task. In MATLAB, functions are defined in separate files. The name of the file and of the function should be the same.

    Functions operate on variables within their own workspace, which is also called the local workspace, separate from the workspace you access at the MATLAB command prompt which is called the base workspace.

    Functions can accept more than one input arguments and may return more than one output arguments.

    Syntax of a function statement is −

    function [out1,out2, ..., outN] = myfun(in1,in2,in3, ..., inN)

    Example

    The following function named mymax should be written in a file named mymax.m. It takes five numbers as argument and returns the maximum of the numbers.

    Create a function file, named mymax.m and type the following code in it −

    function max = mymax(n1, n2, n3, n4, n5)

%This function calculates the maximum of the
% five numbers given as input
max =  n1;
if(n2 > max)
   max = n2;
end
if(n3 > max)
   max = n3;
end
if(n4 > max)
   max = n4;
end
if(n5 > max)
   max = n5;
end

    The first line of a function starts with the keyword function. It gives the name of the function and order of arguments. In our example, the mymax function has five input arguments and one output argument.

    The comment lines that come right after the function statement provide the help text. These lines are printed when you type −

    help mymax

    MATLAB will execute the above statement and return the following result −

    This function calculates the maximum of the
   five numbers given as input

    You can call the function as −

    mymax(34, 78, 89, 23, 11)

    MATLAB will execute the above statement and return the following result −

    ans = 89

    Anonymous Functions

    An anonymous function is like an inline function in traditional programming languages, defined within a single MATLAB statement. It consists of a single MATLAB expression and any number of input and output arguments.

    You can define an anonymous function right at the MATLAB command line or within a function or script.

    This way you can create simple functions without having to create a file for them.

    The syntax for creating an anonymous function from an expression is

    f = @(arglist)expression

    Example

    In this example, we will write an anonymous function named power, which will take two numbers as input and return first number raised to the power of the second number.

    Create a script file and type the following code in it −

    power = @(x, n) x.^n;
result1 = power(7, 3)
result2 = power(49, 0.5)
result3 = power(10, -10)
result4 = power (4.5, 1.5)

    When you run the file, it displays −

    result1 =  343
result2 =  7
result3 =  1.0000e-10
result4 =  9.5459

    Primary and Sub-Functions

    Any function other than an anonymous function must be defined within a file. Each function file contains a required primary function that appears first and any number of optional sub-functions that comes after the primary function and used by it.

    Primary functions can be called from outside of the file that defines them, either from command line or from other functions, but sub-functions cannot be called from command line or other functions, outside the function file.

    Sub-functions are visible only to the primary function and other sub-functions within the function file that defines them.

    Example

    Let us write a function named quadratic that would calculate the roots of a quadratic equation. The function would take three inputs, the quadratic co-efficient, the linear co-efficient and the constant term. It would return the roots.

    The function file quadratic.m will contain the primary function quadratic and the sub-function disc, which calculates the discriminant.

    Create a function file quadratic.m and type the following code in it −

    function [x1,x2] = quadratic(a,b,c)

%this function returns the roots of 
% a quadratic equation.
% It takes 3 input arguments
% which are the co-efficients of x2, x and the 
%constant term
% It returns the roots
d = disc(a,b,c); 
x1 = (-b + d) / (2*a);
x2 = (-b - d) / (2*a);
end   % end of quadratic

function dis = disc(a,b,c) 
%function calculates the discriminant
dis = sqrt(b^2 - 4*a*c);
end   % end of sub-function

    You can call the above function from command prompt as −

    quadratic(2,4,-4)

    MATLAB will execute the above statement and return the following result −

    ans = 0.7321

    Nested Functions

    You can define functions within the body of another function. These are called nested functions. A nested function contains any or all of the components of any other function.

    Nested functions are defined within the scope of another function and they share access to the containing function’s workspace.

    A nested function follows the following syntax −

    function x = A(p1, p2)
...
B(p2)
   function y = B(p3)
   ...
   end
...
end

    Example

    Let us rewrite the function quadratic, from previous example, however, this time the disc function will be a nested function.

    Create a function file quadratic2.m and type the following code in it −

    function [x1,x2] = quadratic2(a,b,c)
function disc  % nested function
d = sqrt(b^2 - 4*a*c);
end   % end of function disc

disc;
x1 = (-b + d) / (2*a);
x2 = (-b - d) / (2*a);
end   % end of function quadratic2

    You can call the above function from command prompt as −

    quadratic2(2,4,-4)

    MATLAB will execute the above statement and return the following result −

    ans =  0.73205

    Private Functions

    A private function is a primary function that is visible only to a limited group of other functions. If you do not want to expose the implementation of a function(s), you can create them as private functions.

    Private functions reside in subfolders with the special name private.

    They are visible only to functions in the parent folder.

    Example

    Let us rewrite the quadratic function. This time, however, the disc function calculating the discriminant, will be a private function.

    Create a subfolder named private in working directory. Store the following function file disc.m in it −

    function dis = disc(a,b,c) 
%function calculates the discriminant
dis = sqrt(b^2 - 4*a*c);
end      % end of sub-function

    Create a function quadratic3.m in your working directory and type the following code in it −

    function [x1,x2] = quadratic3(a,b,c)

%this function returns the roots of 
% a quadratic equation.
% It takes 3 input arguments
% which are the co-efficient of x2, x and the 
%constant term
% It returns the roots
d = disc(a,b,c); 

x1 = (-b + d) / (2*a);
x2 = (-b - d) / (2*a);
end      % end of quadratic3

    You can call the above function from command prompt as −

    quadratic3(2,4,-4)

    MATLAB will execute the above statement and return the following result −

    ans =  0.73205

    Global Variables

    Global variables can be shared by more than one function. For this, you need to declare the variable as global in all the functions.

    If you want to access that variable from the base workspace, then declare the variable at the command line.

    The global declaration must occur before the variable is actually used in a function. It is a good practice to use capital letters for the names of global variables to distinguish them from other variables.

    Example

    Let us create a function file named average.m and type the following code in it −

    function avg = average(nums)
global TOTAL
avg = sum(nums)/TOTAL;
end

    Create a script file and type the following code in it −

    global TOTAL;
TOTAL = 10;
n = [34, 45, 25, 45, 33, 19, 40, 34, 38, 42];
av = average(n)

    When you run the file, it will display the following result −

    av =  35.500

  • Strings

    Creating a character string is quite simple in MATLAB. In fact, we have used it many times. For example, you type the following in the command prompt −

    my_string = 'Tutorials Point'

    MATLAB will execute the above statement and return the following result −

    my_string = Tutorials Point

    MATLAB considers all variables as arrays, and strings are considered as character arrays. Let us use the whos command to check the variable created above −

    whos

    MATLAB will execute the above statement and return the following result −

    Name           Size            Bytes  Class    Attributes
my_string      1x16               32  char

    Interestingly, you can use numeric conversion functions like uint8 or uint16 to convert the characters in the string to their numeric codes. The char function converts the integer vector back to characters −

    Example

    Create a script file and type the following code into it −

    my_string = 'Tutorial''s Point';
str_ascii = uint8(my_string)        % 8-bit ascii values
str_back_to_char= char(str_ascii)  
str_16bit = uint16(my_string)       % 16-bit ascii values
str_back_to_char = char(str_16bit)

    When you run the file, it displays the following result −

    str_ascii =

   84  117  116  111  114  105   97  108   39  115   32   80  111  105  110  116

str_back_to_char = Tutorial's Point
str_16bit =

   84  117  116  111  114  105   97  108   39  115   32   80  111  105  110  116

str_back_to_char = Tutorial's Point

    Rectangular Character Array

    The strings we have discussed so far are one-dimensional character arrays; however, we need to store more than that. We need to store more dimensional textual data in our program. This is achieved by creating rectangular character arrays.

    Simplest way of creating a rectangular character array is by concatenating two or more one-dimensional character arrays, either vertically or horizontally as required.

    You can combine strings vertically in either of the following ways −

    • Using the MATLAB concatenation operator [] and separating each row with a semicolon (;). Please note that in this method each row must contain the same number of characters. For strings with different lengths, you should pad with space characters as needed.
    • Using the char function. If the strings are of different lengths, char pads the shorter strings with trailing blanks so that each row has the same number of characters.

    Example

    Create a script file and type the following code into it −

    doc_profile = ['Zara Ali                             '; ...

               'Sr. Surgeon                          '; ...
           'R N Tagore Cardiology Research Center']
    doc_profile = char('Zara Ali', 'Sr. Surgeon', ...

                  'RN Tagore Cardiology Research Center')</code></pre>
    



    When you run the file, it displays the following result −
    




    doc_profile =
Zara Ali                             
Sr. Surgeon                          
R N Tagore Cardiology Research Center
doc_profile =
Zara Ali                            
Sr. Surgeon                         
RN Tagore Cardiology Research Center

    




    You can combine strings horizontally in either of the following ways −
    




      

    • Using the MATLAB concatenation operator, [] and separating the input strings with a comma or a space. This method preserves any trailing spaces in the input arrays.
      • 




    • Using the string concatenation function, strcat. This method removes trailing spaces in the inputs.
      • 

    




    Example
    




    Create a script file and type the following code into it −
    




    name =     'Zara Ali                             ';
position = 'Sr. Surgeon                          '; 
worksAt =  'R N Tagore Cardiology Research Center';
profile = [name ', ' position ', ' worksAt]
profile = strcat(name, ', ', position, ', ', worksAt)
    




    When you run the file, it displays the following result −
    




    profile = Zara Ali      , Sr. Surgeon      , R N Tagore Cardiology Research Center
profile = Zara Ali,Sr. Surgeon,R N Tagore Cardiology Research Center

    




    Combining Strings into a Cell Array
    




    From our previous discussion, it is clear that combining strings with different lengths could be a pain as all strings in the array has to be of the same length. We have used blank spaces at the end of strings to equalize their length.
    




    However, a more efficient way to combine the strings is to convert the resulting array into a cell array.
    




    MATLAB cell array can hold different sizes and types of data in an array. Cell arrays provide a more flexible way to store strings of varying length.
    




    The cellstr function converts a character array into a cell array of strings.
    




    Example
    




    Create a script file and type the following code into it −
    




    name =     'Zara Ali                             ';
position = 'Sr. Surgeon                          '; 
worksAt =  'R N Tagore Cardiology Research Center';
profile = char(name, position, worksAt);
profile = cellstr(profile);
disp(profile)
    




    When you run the file, it displays the following result −
    




    {                                                                               
   [1,1] = Zara Ali                                                              
   [2,1] = Sr. Surgeon                                                           
   [3,1] = R N Tagore Cardiology Research Center                                 
}   

    




    String Functions in MATLAB
    




    MATLAB provides numerous string functions creating, combining, parsing, comparing and manipulating strings.
    




    Following table provides brief description of the string functions in MATLAB −
    




    FunctionPurpose
    Functions for storing text in character arrays, combine character arrays, etc.
    blanksCreate string of blank characters
    cellstrCreate cell array of strings from character array
    charConvert to character array (string)
    iscellstrDetermine whether input is cell array of strings
    ischarDetermine whether item is character array
    sprintfFormat data into string
    strcatConcatenate strings horizontally
    strjoinJoin strings in cell array into single string
    Functions for identifying parts of strings, find and replace substrings
    ischarDetermine whether item is character array
    isletterArray elements that are alphabetic letters
    isspaceArray elements that are space characters
    isstrpropDetermine whether string is of specified category
    sscanfRead formatted data from string
    strfindFind one string within another
    strrepFind and replace substring
    strsplitSplit string at specified delimiter
    strtokSelected parts of string
    validatestringCheck validity of text string
    symvarDetermine symbolic variables in expression
    regexpMatch regular expression (case sensitive)
    regexpiMatch regular expression (case insensitive)
    regexprepReplace string using regular expression
    regexptranslateTranslate string into regular expression
    Functions for string comparison
    strcmpCompare strings (case sensitive)
    strcmpiCompare strings (case insensitive)
    strncmpCompare first n characters of strings (case sensitive)
    strncmpiCompare first n characters of strings (case insensitive)
    Functions for changing string to upper- or lowercase, creating or removing white space
    deblankStrip trailing blanks from end of string
    strtrimRemove leading and trailing white space from string
    lowerConvert string to lowercase
    upperConvert string to uppercase
    strjustJustify character array
    




    Examples
    




    The following examples illustrate some of the above-mentioned string functions −
    




    Formatting Strings
    




    Create a script file and type the following code into it −
    




    A = pi*1000*ones(1,5);
sprintf(' %f \n %.2f \n %+.2f \n %12.2f \n %012.2f \n', A)
    




    When you run the file, it displays the following result −
    




    ans =  3141.592654 
   3141.59 
   +3141.59 

      3141.59 
       000003141.59 

    




    Joining Strings
    




    Create a script file and type the following code into it −
    




    %cell array of strings
str_array = {'red','blue','green', 'yellow', 'orange'};

% Join strings in cell array into single string
str1 = strjoin(str_array, "-")
str2 = strjoin(str_array, ",")
    




    When you run the file, it displays the following result −
    




    str1 = red-blue-green-yellow-orange
str2 = red,blue,green,yellow,orange

    




    Finding and Replacing Strings
    




    Create a script file and type the following code into it −
    




    students = {'Zara Ali', 'Neha Bhatnagar', ...

            'Monica Malik', 'Madhu Gautam', ...
        'Madhu Sharma', 'Bhawna Sharma',...
        'Nuha Ali', 'Reva Dutta', ...
        'Sunaina Ali', 'Sofia Kabir'};
     
% The strrep function searches and replaces sub-string.
new_student = strrep(students(8), 'Reva', 'Poulomi')
% Display first names
first_names = strtok(students)
    




    When you run the file, it displays the following result −
    




    new_student = 
{
   [1,1] = Poulomi Dutta
}
first_names = 
{
   [1,1] = Zara
   [1,2] = Neha
   [1,3] = Monica
   [1,4] = Madhu
   [1,5] = Madhu
   [1,6] = Bhawna
   [1,7] = Nuha
   [1,8] = Reva
   [1,9] = Sunaina
   [1,10] = Sofia
}

    




    Comparing Strings
    




    Create a script file and type the following code into it −
    




    str1 = 'This is test'
str2 = 'This is text'
if (strcmp(str1, str2))
   sprintf('%s and %s are equal', str1, str2)
else
   sprintf('%s and %s are not equal', str1, str2)
end
    




    When you run the file, it displays the following result −
    




    str1 = This is test
str2 = This is text
ans = This is test and This is text are not equal

  • Numbers

    MATLAB supports various numeric classes that include signed and unsigned integers and single-precision and double-precision floating-point numbers. By default, MATLAB stores all numeric values as double-precision floating point numbers.

    You can choose to store any number or array of numbers as integers or as single-precision numbers.

    All numeric types support basic array operations and mathematical operations.

    Conversion to Various Numeric Data Types

    MATLAB provides the following functions to convert to various numeric data types −

    FunctionPurpose
    doubleConverts to double precision number
    singleConverts to single precision number
    int8Converts to 8-bit signed integer
    int16Converts to 16-bit signed integer
    int32Converts to 32-bit signed integer
    int64Converts to 64-bit signed integer
    uint8Converts to 8-bit unsigned integer
    uint16Converts to 16-bit unsigned integer
    uint32Converts to 32-bit unsigned integer
    uint64Converts to 64-bit unsigned integer

    Example

    Create a script file and type the following code −

    x = single([5.32 3.47 6.28]) .* 7.5
x = double([5.32 3.47 6.28]) .* 7.5
x = int8([5.32 3.47 6.28]) .* 7.5
x = int16([5.32 3.47 6.28]) .* 7.5
x = int32([5.32 3.47 6.28]) .* 7.5
x = int64([5.32 3.47 6.28]) .* 7.5

    When you run the file, it shows the following result −

    x =

   39.900   26.025   47.100

x =

   39.900   26.025   47.100

x =

   38  23  45

x =

   38  23  45

x =

   38  23  45

x =

   38  23  45

    Example

    Let us extend the previous example a little more. Create a script file and type the following code −

    x = int32([5.32 3.47 6.28]) .* 7.5
x = int64([5.32 3.47 6.28]) .* 7.5
x = num2cell(x)

    When you run the file, it shows the following result −

    x =

   38  23  45

x =

   38  23  45

x = 
{
   [1,1] = 38
   [1,2] = 23
   [1,3] = 45
}

    Smallest and Largest Integers

    The functions intmax() and intmin() return the maximum and minimum values that can be represented with all types of integer numbers.

    Both the functions take the integer data type as the argument, for example, intmax(int8) or intmin(int64) and return the maximum and minimum values that you can represent with the integer data type.

    Example

    The following example illustrates how to obtain the smallest and largest values of integers. Create a script file and write the following code in it −

    % displaying the smallest and largest signed integer data
str = 'The range for int8 is:\n\t%d to %d ';
sprintf(str, intmin('int8'), intmax('int8'))

str = 'The range for int16 is:\n\t%d to %d ';
sprintf(str, intmin('int16'), intmax('int16'))

str = 'The range for int32 is:\n\t%d to %d ';
sprintf(str, intmin('int32'), intmax('int32'))

str = 'The range for int64 is:\n\t%d to %d ';
sprintf(str, intmin('int64'), intmax('int64'))
 
% displaying the smallest and largest unsigned integer data
str = 'The range for uint8 is:\n\t%d to %d ';
sprintf(str, intmin('uint8'), intmax('uint8'))

str = 'The range for uint16 is:\n\t%d to %d ';
sprintf(str, intmin('uint16'), intmax('uint16'))

str = 'The range for uint32 is:\n\t%d to %d ';
sprintf(str, intmin('uint32'), intmax('uint32'))

str = 'The range for uint64 is:\n\t%d to %d ';
sprintf(str, intmin('uint64'), intmax('uint64'))

    When you run the file, it shows the following result −

    ans = The range for int8 is:
	-128 to 127 
ans = The range for int16 is:
	-32768 to 32767 
ans = The range for int32 is:
	-2147483648 to 2147483647 
ans = The range for int64 is:
	0 to 0 
ans = The range for uint8 is:
	0 to 255 
ans = The range for uint16 is:
	0 to 65535 
ans = The range for uint32 is:
	0 to -1 
ans = The range for uint64 is:
	0 to 18446744073709551616

    Smallest and Largest Floating Point Numbers

    The functions realmax() and realmin() return the maximum and minimum values that can be represented with floating point numbers.

    Both the functions when called with the argument ‘single’, return the maximum and minimum values that you can represent with the single-precision data type and when called with the argument ‘double’, return the maximum and minimum values that you can represent with the double-precision data type.

    Example

    The following example illustrates how to obtain the smallest and largest floating point numbers. Create a script file and write the following code in it −

    % displaying the smallest and largest single-precision 
% floating point number
str = 'The range for single is:\n\t%g to %g and\n\t %g to  %g';
sprintf(str, -realmax('single'), -realmin('single'), ...
   realmin('single'), realmax('single'))

% displaying the smallest and largest double-precision 
% floating point number
str = 'The range for double is:\n\t%g to %g and\n\t %g to  %g';
sprintf(str, -realmax('double'), -realmin('double'), ...
   realmin('double'), realmax('double'))

    When you run the file, it displays the following result −

    ans = The range for single is:                                                  

        -3.40282e+38 to -1.17549e-38 and                                        
     1.17549e-38 to  3.40282e+38                                            
    ans = The range for double is:                                                  

        -1.79769e+308 to -2.22507e-308 and                                      
     2.22507e-308 to  1.79769e+308</code></pre>

  • Colon Notation

    The colon(:) is one of the most useful operator in MATLAB. It is used to create vectors, subscript arrays, and specify for iterations.

    If you want to create a row vector, containing integers from 1 to 10, you write −

    1:10

    MATLAB executes the statement and returns a row vector containing the integers from 1 to 10 −

    ans =                                                                           

                                                                                
       1    2    3    4    5    6    7    8    9   10

    If you want to specify an increment value other than one, for example −

    100: -5: 50

    MATLAB executes the statement and returns the following result −

    ans =
   100    95    90    85    80    75    70    65    60    55    50

    Let us take another example −

    0:pi/8:pi

    MATLAB executes the statement and returns the following result −

    ans =
   Columns 1 through 7

      0    0.3927    0.7854    1.1781    1.5708    1.9635    2.3562
       Columns 8 through 9

      2.7489    3.1416

    You can use the colon operator to create a vector of indices to select rows, columns or elements of arrays.

    The following table describes its use for this purpose (let us have a matrix A) −

    FormatPurpose
    A(:,j)is the jth column of A.
    A(i,:)is the ith row of A.
    A(:,:)is the equivalent two-dimensional array. For matrices this is the same as A.
    A(j:k)is A(j), A(j+1),…,A(k).
    A(:,j:k)is A(:,j), A(:,j+1),…,A(:,k).
    A(:,:,k)is the kth page of three-dimensional array A.
    A(i,j,k,:)is a vector in four-dimensional array A. The vector includes A(i,j,k,1), A(i,j,k,2), A(i,j,k,3), and so on.
    A(:)is all the elements of A, regarded as a single column. On the left side of an assignment statement, A(:) fills A, preserving its shape from before. In this case, the right side must contain the same number of elements as A.

    Example

    Create a script file and type the following code in it −

    A = [1 2 3 4; 4 5 6 7; 7 8 9 10]
A(:,2)      % second column of A
A(:,2:3)    % second and third column of A
A(2:3,2:3)  % second and third rows and second and third columns

    When you run the file, it displays the following result −

    A =

      1     2     3     4
  4     5     6     7
  7     8     9    10
    
ans =

      2
  5
  8
    
ans =

      2     3
  5     6
  8     9
    
ans =

      5     6
  8     9

  • Arrays

    All variables of all data types in MATLAB are multidimensional arrays. A vector is a one-dimensional array and a matrix is a two-dimensional array.

    We have already discussed vectors and matrices. In this chapter, we will discuss multidimensional arrays. However, before that, let us discuss some special types of arrays.

    Special Arrays in MATLAB

    In this section, we will discuss some functions that create some special arrays. For all these functions, a single argument creates a square array, double arguments create rectangular array.

    The zeros() function creates an array of all zeros −

    For example −

    zeros(5)

    MATLAB will execute the above statement and return the following result −

    ans =

      0     0     0     0     0
  0     0     0     0     0
  0     0     0     0     0
  0     0     0     0     0
  0     0     0     0     0

    The ones() function creates an array of all ones −

    For example −

    ones(4,3)

    MATLAB will execute the above statement and return the following result −

    ans =

      1     1     1
  1     1     1
  1     1     1
  1     1     1

    The eye() function creates an identity matrix.

    For example −

    eye(4)

    MATLAB will execute the above statement and return the following result −

    ans =

      1     0     0     0
  0     1     0     0
  0     0     1     0
  0     0     0     1

    The rand() function creates an array of uniformly distributed random numbers on (0,1) −

    For example −

    rand(3, 5)

    MATLAB will execute the above statement and return the following result −

    ans =
   0.8147    0.9134    0.2785    0.9649    0.9572
   0.9058    0.6324    0.5469    0.1576    0.4854
   0.1270    0.0975    0.9575    0.9706    0.8003

    A Magic Square

    A magic square is a square that produces the same sum, when its elements are added row-wise, column-wise or diagonally.

    The magic() function creates a magic square array. It takes a singular argument that gives the size of the square. The argument must be a scalar greater than or equal to 3.

    magic(4)

    MATLAB will execute the above statement and return the following result −

    ans =
   16     2     3    13
   5    11    10     8
   9     7     6    12
   4    14    15     1

    Multidimensional Arrays

    An array having more than two dimensions is called a multidimensional array in MATLAB. Multidimensional arrays in MATLAB are an extension of the normal two-dimensional matrix.

    Generally to generate a multidimensional array, we first create a two-dimensional array and extend it.

    For example, let’s create a two-dimensional array a.

    a = [7 9 5; 6 1 9; 4 3 2]

    MATLAB will execute the above statement and return the following result −

    a =
   7     9     5
   6     1     9
   4     3     2

    The array a is a 3-by-3 array; we can add a third dimension to a, by providing the values like −

    a(:, :, 2)= [ 1 2 3; 4 5 6; 7 8 9]

    MATLAB will execute the above statement and return the following result −

    a =

ans(:,:,1) =

   0   0   0
   0   0   0
   0   0   0

ans(:,:,2) =

   1   2   3
   4   5   6
   7   8   9

    We can also create multidimensional arrays using the ones(), zeros() or the rand() functions.

    For example,

    b = rand(4,3,2)

    MATLAB will execute the above statement and return the following result −

    b(:,:,1) =
   0.0344    0.7952    0.6463
   0.4387    0.1869    0.7094
   0.3816    0.4898    0.7547
   0.7655    0.4456    0.2760

b(:,:,2) =
   0.6797    0.4984    0.2238
   0.6551    0.9597    0.7513
   0.1626    0.3404    0.2551
   0.1190    0.5853    0.5060

    We can also use the cat() function to build multidimensional arrays. It concatenates a list of arrays along a specified dimension −

    Syntax for the cat() function is −

    B = cat(dim, A1, A2...)

    Where,

    • B is the new array created
    • A1, A2, … are the arrays to be concatenated
    • dim is the dimension along which to concatenate the arrays

    Example

    Create a script file and type the following code into it −

    a = [9 8 7; 6 5 4; 3 2 1];
b = [1 2 3; 4 5 6; 7 8 9];
c = cat(3, a, b, [ 2 3 1; 4 7 8; 3 9 0])

    When you run the file, it displays −

    c(:,:,1) =

      9     8     7
  6     5     4
  3     2     1
    c(:,:,2) =

      1     2     3
  4     5     6
  7     8     9
    c(:,:,3) =

      2     3     1
  4     7     8
  3     9     0

    Array Functions

    MATLAB provides the following functions to sort, rotate, permute, reshape, or shift array contents.

    FunctionPurpose
    lengthLength of vector or largest array dimension
    ndimsNumber of array dimensions
    numelNumber of array elements
    sizeArray dimensions
    iscolumnDetermines whether input is column vector
    isemptyDetermines whether array is empty
    ismatrixDetermines whether input is matrix
    isrowDetermines whether input is row vector
    isscalarDetermines whether input is scalar
    isvectorDetermines whether input is vector
    blkdiagConstructs block diagonal matrix from input arguments
    circshiftShifts array circularly
    ctransposeComplex conjugate transpose
    diagDiagonal matrices and diagonals of matrix
    flipdimFlips array along specified dimension
    fliplrFlips matrix from left to right
    flipudFlips matrix up to down
    ipermuteInverses permute dimensions of N-D array
    permuteRearranges dimensions of N-D array
    repmatReplicates and tile array
    reshapeReshapes array
    rot90Rotates matrix 90 degrees
    shiftdimShifts dimensions
    issortedDetermines whether set elements are in sorted order
    sortSorts array elements in ascending or descending order
    sortrowsSorts rows in ascending order
    squeezeRemoves singleton dimensions
    transposeTranspose
    vectorizeVectorizes expression

    Examples

    The following examples illustrate some of the functions mentioned above.

    Length, Dimension and Number of elements −

    Create a script file and type the following code into it −

    x = [7.1, 3.4, 7.2, 28/4, 3.6, 17, 9.4, 8.9];
length(x)      % length of x vector
y = rand(3, 4, 5, 2);
ndims(y)       % no of dimensions in array y
s = ['Zara', 'Nuha', 'Shamim', 'Riz', 'Shadab'];
numel(s)       % no of elements in s

    When you run the file, it displays the following result −

    ans =  8
ans =  4
ans =  23

    Circular Shifting of the Array Elements −

    Create a script file and type the following code into it −

    a = [1 2 3; 4 5 6; 7 8 9]  % the original array a
b = circshift(a,1)         %  circular shift first dimension values down by 1.
c = circshift(a,[1 -1])    % circular shift first dimension values % down by 1 

                           % and second dimension values to the left % by 1.</code></pre>
    



    When you run the file, it displays the following result −
    




    a =
   1     2     3
   4     5     6
   7     8     9

b =
   7     8     9
   1     2     3
   4     5     6

c =
   8     9     7
   2     3     1
   5     6     4

    




    Sorting Arrays
    




    Create a script file and type the following code into it −
    




    v = [ 23 45 12 9 5 0 19 17]  % horizontal vector
sort(v)                      % sorting v
m = [2 6 4; 5 3 9; 2 0 1]    % two dimensional array
sort(m, 1)                   % sorting m along the row
sort(m, 2)                   % sorting m along the column
    




    When you run the file, it displays the following result −
    




    

    

    v =
   23    45    12     9     5     0    19    17
ans =
   0     5     9    12    17    19    23    45
m =
   2     6     4
   5     3     9
   2     0     1
ans =
   2     0     1
   2     3     4
   5     6     9
ans =
   2     4     6
   3     5     9
   0     1     2

    

    

    




    Cell Array
    




    Cell arrays are arrays of indexed cells where each cell can store an array of a different dimensions and data types.
    




    The cell function is used for creating a cell array. Syntax for the cell function is −
    




    C = cell(dim)
C = cell(dim1,...,dimN)
D = cell(obj)
    




    Where,
    




      

    • C is the cell array;
      • 




    • dim is a scalar integer or vector of integers that specifies the dimensions of cell array C;
      • 




    • dim1, ... , dimN are scalar integers that specify the dimensions of C;
      • 




    • obj is One of the following −

        

      • Java array or object
        • 




      • .NET array of type System.String or System.Object
        • 

      

      • 

    




    Example
    




    Create a script file and type the following code into it −
    




    c = cell(2, 5);
c = {'Red', 'Blue', 'Green', 'Yellow', 'White'; 1 2 3 4 5}
    




    When you run the file, it displays the following result −
    




    c = 
{
   [1,1] = Red
   [2,1] =  1
   [1,2] = Blue
   [2,2] =  2
   [1,3] = Green
   [2,3] =  3
   [1,4] = Yellow
   [2,4] =  4
   [1,5] = White
   [2,5] =  5
}

    




    Accessing Data in Cell Arrays
    




    There are two ways to refer to the elements of a cell array −
    




      

    • Enclosing the indices in first bracket (), to refer to sets of cells
      • 




    • Enclosing the indices in braces {}, to refer to the data within individual cells
      • 

    




    When you enclose the indices in first bracket, it refers to the set of cells.
    




    Cell array indices in smooth parentheses refer to sets of cells.
    




    For example −
    




    c = {'Red', 'Blue', 'Green', 'Yellow', 'White'; 1 2 3 4 5};
c(1:2,1:2)
    




    MATLAB will execute the above statement and return the following result −
    




    ans = 
{
   [1,1] = Red
   [2,1] =  1
   [1,2] = Blue
   [2,2] =  2
}

    




    You can also access the contents of cells by indexing with curly braces.
    




    For example −
    




    c = {'Red', 'Blue', 'Green', 'Yellow', 'White'; 1 2 3 4 5};
c{1, 2:4}
    




    MATLAB will execute the above statement and return the following result −
    




    ans = Blue
ans = Green
ans = Yellow

  • Matrix

    A matrix is a two-dimensional array of numbers.

    In MATLAB, you create a matrix by entering elements in each row as comma or space delimited numbers and using semicolons to mark the end of each row.

    For example, let us create a 4-by-5 matrix a −

    a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8]

    MATLAB will execute the above statement and return the following result −

    a =

      1     2     3     4     5
  2     3     4     5     6
  3     4     5     6     7
  4     5     6     7     8

    Referencing the Elements of a Matrix

    To reference an element in the mth row and nth column, of a matrix mx, we write −

    mx(m, n);

    For example, to refer to the element in the 2nd row and 5th column, of the matrix a, as created in the last section, we type −

    a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(2,5)

    MATLAB will execute the above statement and return the following result −

    ans =  6

    To reference all the elements in the mth column we type A(:,m).

    Let us create a column vector v, from the elements of the 4th row of the matrix a −

    a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
v = a(:,4)

    MATLAB will execute the above statement and return the following result −

    v =

      4
  5
  6
  7

    You can also select the elements in the mth through nth columns, for this we write −

    a(:,m:n)

    Let us create a smaller matrix taking the elements from the second and third columns −

    a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(:, 2:3)

    MATLAB will execute the above statement and return the following result −

    ans =

      2     3
  3     4
  4     5
  5     6

    In the same way, you can create a sub-matrix taking a sub-part of a matrix.

    a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(:, 2:3)

    MATLAB will execute the above statement and return the following result −

    ans =

      2     3
  3     4
  4     5
  5     6

    In the same way, you can create a sub-matrix taking a sub-part of a matrix.

    For example, let us create a sub-matrix sa taking the inner subpart of a −

    3     4     5     
4     5     6

    To do this, write −

    a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
sa = a(2:3,2:4)

    MATLAB will execute the above statement and return the following result −

    sa =

      3     4     5
  4     5     6

    Deleting a Row or a Column in a Matrix

    You can delete an entire row or column of a matrix by assigning an empty set of square braces [] to that row or column. Basically, [] denotes an empty array.

    For example, let us delete the fourth row of a −

    a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a( 4 , : ) = []

    MATLAB will execute the above statement and return the following result −

    a =

      1     2     3     4     5
  2     3     4     5     6
  3     4     5     6     7

    Next, let us delete the fifth column of a −

    a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(: , 5)=[]

    MATLAB will execute the above statement and return the following result −

    a =

      1     2     3     4
  2     3     4     5
  3     4     5     6
  4     5     6     7

    Example

    In this example, let us create a 3-by-3 matrix m, then we will copy the second and third rows of this matrix twice to create a 4-by-3 matrix.

    Create a script file with the following code −

    a = [ 1 2 3 ; 4 5 6; 7 8 9];
new_mat = a([2,3,2,3],:)

    When you run the file, it displays the following result −

    new_mat =

      4     5     6
  7     8     9
  4     5     6
  7     8     9

  • Vectors

    A vector is a one-dimensional array of numbers. MATLAB allows creating two types of vectors −

    • Row vectors
    • Column vectors

    Row Vectors

    Row vectors are created by enclosing the set of elements in square brackets, using space or comma to delimit the elements.

    r = [7 8 9 10 11]

    MATLAB will execute the above statement and return the following result −

    r =

   7    8    9   10   11

    Column Vectors

    Column vectors are created by enclosing the set of elements in square brackets, using semicolon to delimit the elements.

    c = [7;  8;  9;  10; 11]

    MATLAB will execute the above statement and return the following result −

    c =

      7       
  8       
  9       
  10       
  11

    Referencing the Elements of a Vector

    You can reference one or more of the elements of a vector in several ways. The ith component of a vector v is referred as v(i). For example −

    v = [ 1; 2; 3; 4; 5; 6];	% creating a column vector of 6 elements
v(3)

    MATLAB will execute the above statement and return the following result −

    ans =  3

    When you reference a vector with a colon, such as v(:), all the components of the vector are listed.

    v = [ 1; 2; 3; 4; 5; 6];	% creating a column vector of 6 elements
v(:)

    MATLAB will execute the above statement and return the following result −

    ans =

     1
 2
 3
 4
 5
 6

    MATLAB allows you to select a range of elements from a vector.

    For example, let us create a row vector rv of 9 elements, then we will reference the elements 3 to 7 by writing rv(3:7) and create a new vector named sub_rv.

    rv = [1 2 3 4 5 6 7 8 9];
sub_rv = rv(3:7)

    MATLAB will execute the above statement and return the following result −

    sub_rv =

   3   4   5   6   7

  • Loop Types

    There may be a situation when you need to execute a block of code several number of times. In general, statements are executed sequentially. The first statement in a function is executed first, followed by the second, and so on.

    Programming languages provide various control structures that allow for more complicated execution paths.

    A loop statement allows us to execute a statement or group of statements multiple times and following is the general form of a loop statement in most of the programming languages −

    Loop Architecture

    MATLAB provides following types of loops to handle looping requirements. Click the following links to check their detail −

    Sr.No.Loop Type & Description
    1while loopRepeats a statement or group of statements while a given condition is true. It tests the condition before executing the loop body.
    2for loopExecutes a sequence of statements multiple times and abbreviates the code that manages the loop variable.
    3nested loopsYou can use one or more loops inside any another loop.

    Loop Control Statements

    Loop control statements change execution from its normal sequence. When execution leaves a scope, all automatic objects that were created in that scope are destroyed.

    MATLAB supports the following control statements. Click the following links to check their detail.

    Sr.No.Control Statement & Description
    1break statementTerminates the loop statement and transfers execution to the statement immediately following the loop.
    2continue statementCauses the loop to skip the remainder of its body and immediately retest its condition prior to reiterating.

  • Decision Making

    Decision making structures require that the programmer should specify one or more conditions to be evaluated or tested by the program, along with a statement or statements to be executed if the condition is determined to be true, and optionally, other statements to be executed if the condition is determined to be false.

    Following is the general form of a typical decision making structure found in most of the programming languages −

    Decision making statements in MATLAB

    MATLAB provides following types of decision making statements. Click the following links to check their detail −

    Sr.No.Statement & Description
    1if … end statementAn if … end statement consists of a boolean expression followed by one or more statements.
    2if…else…end statementAn if statement can be followed by an optional else statement, which executes when the boolean expression is false.
    3If… elseif…elseif…else…end statementsAn if statement can be followed by one (or more) optional elseif… and an else statement, which is very useful to test various conditions.
    4nested if statementsYou can use one if or elseif statement inside another if or elseif statement(s).
    5switch statementA switch statement allows a variable to be tested for equality against a list of values.
    6nested switch statementsYou can use one switch statement inside another switch statement(s).

  • Operators

    An operator is a symbol that tells the compiler to perform specific mathematical or logical manipulations. MATLAB is designed to operate primarily on whole matrices and arrays. Therefore, operators in MATLAB work both on scalar and non-scalar data. MATLAB allows the following types of elementary operations −

    • Arithmetic Operators
    • Relational Operators
    • Logical Operators
    • Bitwise Operations
    • Set Operations

    Arithmetic Operators

    MATLAB allows two different types of arithmetic operations −

    • Matrix arithmetic operations
    • Array arithmetic operations

    Matrix arithmetic operations are same as defined in linear algebra. Array operations are executed element by element, both on one-dimensional and multidimensional array.

    The matrix operators and array operators are differentiated by the period (.) symbol. However, as the addition and subtraction operation is same for matrices and arrays, the operator is same for both cases. The following table gives brief description of the operators −

    Sr.No.Operator & Description
    1+Addition or unary plus. A+B adds the values stored in variables A and B. A and B must have the same size, unless one is a scalar. A scalar can be added to a matrix of any size.
    2–Subtraction or unary minus. A-B subtracts the value of B from A. A and B must have the same size, unless one is a scalar. A scalar can be subtracted from a matrix of any size.
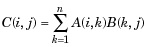    3*Matrix multiplication. C = A*B is the linear algebraic product of the matrices A and B. More precisely,Matrix MultiplicationFor non-scalar A and B, the number of columns of A must be equal to the number of rows of B. A scalar can multiply a matrix of any size.
    4.*Array multiplication. A.*B is the element-by-element product of the arrays A and B. A and B must have the same size, unless one of them is a scalar.
    5/Slash or matrix right division. B/A is roughly the same as B*inv(A). More precisely, B/A = (A’\B’)’.
    6./Array right division. A./B is the matrix with elements A(i,j)/B(i,j). A and B must have the same size, unless one of them is a scalar.
    7\Backslash or matrix left division. If A is a square matrix, A\B is roughly the same as inv(A)*B, except it is computed in a different way. If A is an n-by-n matrix and B is a column vector with n components, or a matrix with several such columns, then X = A\B is the solution to the equation AX = B. A warning message is displayed if A is badly scaled or nearly singular.
    8.\Array left division. A.\B is the matrix with elements B(i,j)/A(i,j). A and B must have the same size, unless one of them is a scalar.
    9^Matrix power. X^p is X to the power p, if p is a scalar. If p is an integer, the power is computed by repeated squaring. If the integer is negative, X is inverted first. For other values of p, the calculation involves eigenvalues and eigenvectors, such that if [V,D] = eig(X), then X^p = V*D.^p/V.
    10.^Array power. A.^B is the matrix with elements A(i,j) to the B(i,j) power. A and B must have the same size, unless one of them is a scalar.
    11‘Matrix transpose. A’ is the linear algebraic transpose of A. For complex matrices, this is the complex conjugate transpose.
    12.’Array transpose. A.’ is the array transpose of A. For complex matrices, this does not involve conjugation.

    Relational Operators

    Relational operators can also work on both scalar and non-scalar data. Relational operators for arrays perform element-by-element comparisons between two arrays and return a logical array of the same size, with elements set to logical 1 (true) where the relation is true and elements set to logical 0 (false) where it is not.

    The following table shows the relational operators available in MATLAB −

    Sr.No.Operator & Description
    1<Less than
    2<=Less than or equal to
    3>Greater than
    4>=Greater than or equal to
    5==Equal to
    6~=Not equal to

    Logical Operators

    MATLAB offers two types of logical operators and functions −

    • Element-wise − These operators operate on corresponding elements of logical arrays.
    • Short-circuit − These operators operate on scalar and, logical expressions.

    Element-wise logical operators operate element-by-element on logical arrays. The symbols &, |, and ~ are the logical array operators AND, OR, and NOT.

    Short-circuit logical operators allow short-circuiting on logical operations. The symbols && and || are the logical short-circuit operators AND and OR.

    Bitwise Operations

    Bitwise operators work on bits and perform bit-by-bit operation. The truth tables for &, |, and ^ are as follows −

    pqp & qp | qp ^ q
    00000
    01011
    11110
    10011

    Assume if A = 60; and B = 13; Now in binary format they will be as follows −

    A = 0011 1100

    B = 0000 1101

    —————–

    A&B = 0000 1100

    A|B = 0011 1101

    A^B = 0011 0001

    ~A  = 1100 0011

    MATLAB provides various functions for bit-wise operations like ‘bitwise and’, ‘bitwise or’ and ‘bitwise not’ operations, shift operation, etc.

    The following table shows the commonly used bitwise operations −

    FunctionPurpose
    bitand(a, b)Bit-wise AND of integers a and b
    bitcmp(a)Bit-wise complement of a
    bitget(a,pos)Get bit at specified position pos, in the integer array a
    bitor(a, b)Bit-wise OR of integers a and b
    bitset(a, pos)Set bit at specific location pos of a
    bitshift(a, k)Returns a shifted to the left by k bits, equivalent to multiplying by 2k. Negative values of k correspond to shifting bits right or dividing by 2|k| and rounding to the nearest integer towards negative infinite. Any overflow bits are truncated.
    bitxor(a, b)Bit-wise XOR of integers a and b
    swapbytesSwap byte ordering

    Set Operations

    MATLAB provides various functions for set operations, like union, intersection and testing for set membership, etc.

    The following table shows some commonly used set operations −

    Sr.No.Function & Description
    1intersect(A,B)Set intersection of two arrays; returns the values common to both A and B. The values returned are in sorted order.
    2intersect(A,B,’rows’)Treats each row of A and each row of B as single entities and returns the rows common to both A and B. The rows of the returned matrix are in sorted order.
    3ismember(A,B)Returns an array the same size as A, containing 1 (true) where the elements of A are found in B. Elsewhere, it returns 0 (false).
    4ismember(A,B,’rows’)Treats each row of A and each row of B as single entities and returns a vector containing 1 (true) where the rows of matrix A are also rows of B. Elsewhere, it returns 0 (false).
    5issorted(A)Returns logical 1 (true) if the elements of A are in sorted order and logical 0 (false) otherwise. Input A can be a vector or an N-by-1 or 1-by-N cell array of strings. A is considered to be sorted if A and the output of sort(A) are equal.
    6issorted(A, ‘rows’)Returns logical 1 (true) if the rows of two-dimensional matrix A is in sorted order, and logical 0 (false) otherwise. Matrix A is considered to be sorted if A and the output of sortrows(A) are equal.
    7setdiff(A,B)Sets difference of two arrays; returns the values in A that are not in B. The values in the returned array are in sorted order.
    8setdiff(A,B,’rows’)Treats each row of A and each row of B as single entities and returns the rows from A that are not in B. The rows of the returned matrix are in sorted order.The ‘rows’ option does not support cell arrays.
    9setxorSets exclusive OR of two arrays
    10unionSets union of two arrays
    11uniqueUnique values in array