Introduction to Fluid Mechanics

1.1. Fluid Mechanics in Chemical Engineering

Aknowledge of fluid mechanics is essential for the chemical engineer because the majority of chemical-processing operations are conducted either partly or totally in the fluid phase. Examples of such operations abound in the biochemical, chemical, energy, fermentation, materials, mining, petroleum, pharmaceuticals, polymer, and waste-processing industries.

There are two principal reasons for placing such an emphasis on fluids. First, at typical operating conditions, an enormous number of materials normally exist as gases or liquids, or can be transformed into such phases. Second, it is usually more efficient and cost-effective to work with fluids in contrast to solids. Even some operations with solids can be conducted in a quasi-fluidlike manner; examples are the fluidized-bed catalytic refining of hydrocarbons, and the long-distance pipelining of coal particles using water as the agitating and transporting medium.

Although there is inevitably a significant amount of theoretical development, almost all the material in this book has some application to chemical processing and other important practical situations. Throughout, we shall endeavor to present an understanding of the physical behavior involved; only then is it really possible to comprehend the accompanying theory and equations.

1.2. General Concepts of a Fluid

We must begin by responding to the question, “What is a fluid?” Broadly speaking, a fluid is a substance that will deform continuously when it is subjected to a tangential or shear force, much as a similar type of force is exerted when a water-skier skims over the surface of a lake or butter is spread on a slice of bread. The rate at which the fluid deforms continuously depends not only on the magnitude of the applied force but also on a property of the fluid called its viscosity or resistance to deformation and flow. Solids will also deform when sheared, but a position of equilibrium is soon reached in which elastic forces induced by the deformation of the solid exactly counterbalance the applied shear force, and further deformation ceases.

A simple apparatus for shearing a fluid is shown in Fig. 1.1. The fluid is contained between two concentric cylinders; the outer cylinder is stationary, and the inner one (of radius R) is rotated steadily with an angular velocity ω. This shearing motion of a fluid can continue indefinitely, provided that a source of energy—supplied by means of a torque here—is available for rotating the inner cylinder. The diagram also shows the resulting velocity profile; note that the velocity in the direction of rotation varies from the peripheral velocity Rω of the inner cylinder down to zero at the outer stationary cylinder, these representing typical no-slip conditions at both locations. However, if the intervening space is filled with a solid—even one with obvious elasticity, such as rubber—only a limited rotation will be possible before a position of equilibrium is reached, unless, of course, the torque is so high that slip occurs between the rubber and the cylinder.

Fig. 1.1 Shearing of a fluid.

There are various classes of fluids. Those that behave according to nice and obvious simple laws, such as water, oil, and air, are generally called Newtonian fluids. These fluids exhibit constant viscosity but, under typical processing conditions, virtually no elasticity. Fortunately, a very large number of fluids of interest to the chemical engineer exhibit Newtonian behavior, which will be assumed throughout the book, except in Chapter 11, which is devoted to the study of non-Newtonian fluids.

A fluid whose viscosity is not constant (but depends, for example, on the intensity to which it is being sheared), or which exhibits significant elasticity, is termed non-Newtonian. For example, several polymeric materials subject to deformation can “remember” their recent molecular configurations, and in attempting to recover their recent states, they will exhibit elasticity in addition to viscosity. Other fluids, such as drilling mud and toothpaste, behave essentially as solids and will not flow when subject to small shear forces, but will flow readily under the influence of high shear forces.

Fluids can also be broadly classified into two main categories—liquids and gases. Liquids are characterized by relatively high densities and viscosities, with molecules close together; their volumes tend to remain constant, roughly independent of pressure, temperature, or the size of the vessels containing them. Gases, on the other hand, have relatively low densities and viscosities, with molecules far apart; generally, they will rapidly tend to fill the container in which they are placed. However, these two states—liquid and gaseous—represent but the two extreme ends of a continuous spectrum of possibilities.

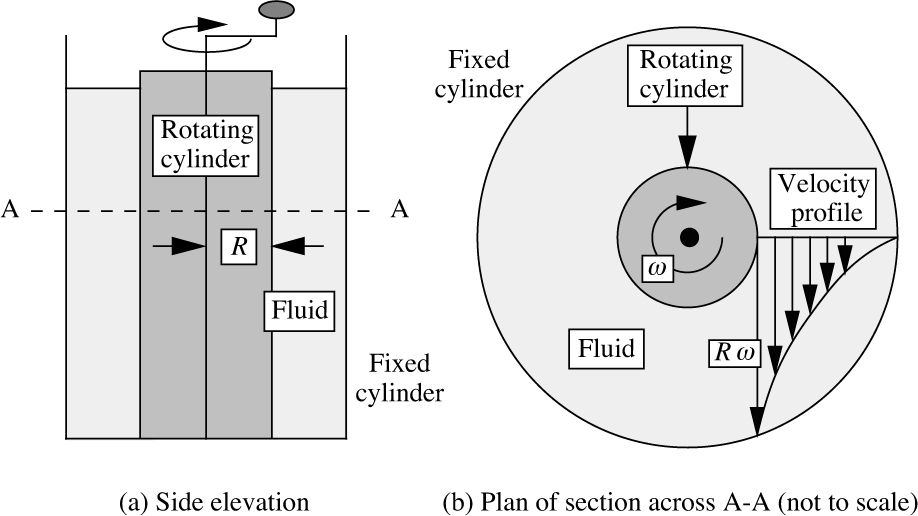
The situation is readily illustrated by considering a fluid that is initially a gas at point G on the pressure/temperature diagram shown in Fig. 1.2. By increasing the pressure, and perhaps lowering the temperature, the vapor-pressure curve is soon reached and crossed, and the fluid condenses and apparently becomes a liquid at point L. By continuously adjusting the pressure and temperature so that the clockwise path is followed, and circumnavigating the critical point C in the process, the fluid is returned to G, where it is presumably once more a gas. But where does the transition from liquid at L to gas at G occur? The answer is at no single point, but rather that the change is a continuous and gradual one, through a whole spectrum of intermediate states.

Fig. 1.2 When does a liquid become a gas?

1.3. Stresses, Pressure, Velocity, and the Basic Laws

Stresses. The concept of a force should be readily apparent. In fluid mechanics, a force per unit area, called a stress, is usually found to be a more convenient and versatile quantity than the force itself. Further, when considering a specific surface, there are two types of stresses that are particularly important.

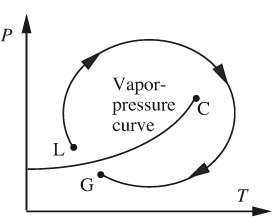
1. The first type of stress, shown in Fig. 1.3(a), acts perpendicularly to the surface and is therefore called a normal stress; it will be tensile or compressive, depending on whether it tends to stretch or to compress the fluid on which it acts. The normal stress equals F/A, where F is the normal force and A is the area of the surface on which it acts. The dotted outlines show the volume changes caused by deformation. In fluid mechanics, pressure is usually the most important type of compressive stress, and will shortly be discussed in more detail.

Fig. 1.3(a) Tensile and compressive normal stresses F/A, acting on a cylinder, causing elongation and shrinkage, respectively.

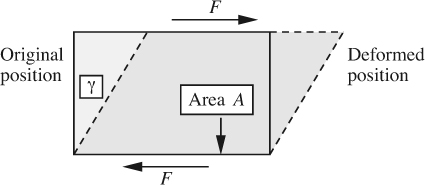
2. The second type of stress, shown in Fig. 1.3(b), acts tangentially to the surface; it is called a shear stress τ, and equals F/A, where F is the tangential force and A is the area on which it acts. Shear stress is transmitted through a fluid by interaction of the molecules with one another. A knowledge of the shear stress is very important when studying the flow of viscous Newtonian fluids. For a given rate of deformation, measured by the time derivative dγ/dt of the small angle of deformation γ, the shear stress τ is directly proportional to the viscosity of the fluid (see Fig. 1.3(b)).

Fig. 1.3(b) Shear stress τ = F/A, acting on a rectangular parallelepiped, shown in cross section, causing a deformation measured by the angle γ (whose magnitude is exaggerated here).

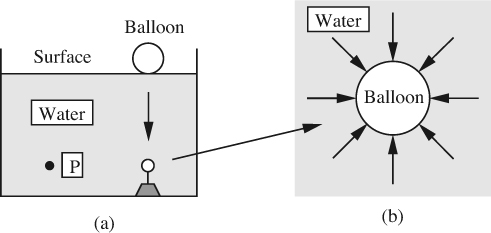
Pressure. In virtually all hydrostatic situations—those involving fluids at rest—the fluid molecules are in a state of compression. For example, for the swimming pool whose cross section is depicted in Fig. 1.4, this compression at a typical point P is caused by the downwards gravitational weight of the water above point P. The degree of compression is measured by a scalar, p—the pressure.

Fig. 1.4 (a) Balloon submerged in a swimming pool; (b) enlarged view of the compressed balloon, with pressure forces acting on it.

A small inflated spherical balloon pulled down from the surface and tethered at the bottom by a weight will still retain its spherical shape (apart from a small distortion at the point of the tether), but will be diminished in size, as in Fig. 1.4(a). It is apparent that there must be forces acting normally inward on the surface of the balloon, and that these must essentially be uniform for the shape to remain spherical, as in Fig. 1.4(b).

Although the pressure p is a scalar, it typically appears in tandem with an area A (assumed small enough so that the pressure is uniform over it). By definition of pressure, the surface experiences a normal compressive force F = pA. Thus, pressure has units of a force per unit area—the same as a stress.

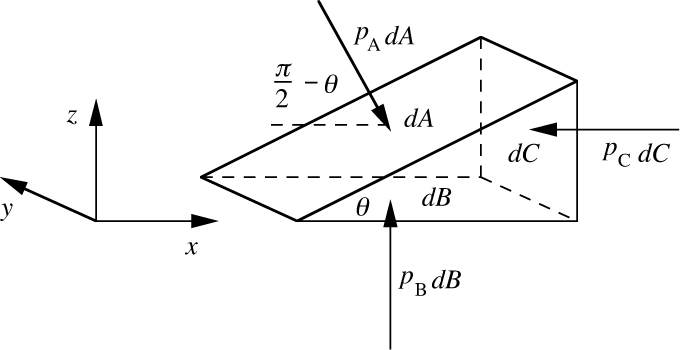
The value of the pressure at a point is independent of the orientation of any area associated with it, as can be deduced with reference to a differentially small wedge-shaped element of the fluid, shown in Fig. 1.5.

Fig. 1.5 Equilibrium of a wedge of fluid.

Due to the pressure there are three forces, p_AdA, p_BdB, and p_CdC, that act on the three rectangular faces of areas dA, dB, and dC. Since the wedge is not moving, equate the two forces acting on it in the horizontal or x direction, noting that p_AdA must be resolved through an angle (π/2 – θ) by multiplying it by cos(π/2 – θ) = sin θ:

The vertical force p_BdB acting on the bottom surface is omitted from Eqn. (1.1) because it has no component in the x direction. The horizontal pressure forces acting in the y direction on the two triangular faces of the wedge are also omitted, since again these forces have no effect in the x direction. From geometrical considerations, areas dA and dC are related by:

These last two equations yield:

verifying that the pressure is independent of the orientation of the surface being considered. A force balance in the z direction leads to a similar result, p_A = p_B.¹

¹ Actually, a force balance in the z direction demands that the gravitational weight of the wedge be considered, which is proportional to the volume of the wedge. However, the pressure forces are proportional to the areas of the faces. It can readily be shown that the volume-to-area effect becomes vanishingly small as the wedge becomes infinitesimally small, so that the gravitational weight is inconsequential.

For moving fluids, the normal stresses include both a pressure and extra stresses caused by the motion of the fluid, as discussed in detail in Section 5.6.

The amount by which a certain pressure exceeds that of the atmosphere is termed the gauge pressure, the reason being that many common pressure gauges are really differential instruments, reading the difference between a required pressure and that of the surrounding atmosphere. Absolute pressure equals the gauge pressure plus the atmospheric pressure.

Velocity. Many problems in fluid mechanics deal with the velocity of the fluid at a point, equal to the rate of change of the position of a fluid particle with time, thus having both a magnitude and a direction. In some situations, particularly those treated from the macroscopic viewpoint, as in Chapters 2, 3, and 4, it sometimes suffices to ignore variations of the velocity with position. In other cases—particularly those treated from the microscopic viewpoint, as in Chapter 6 and later—it is invariably essential to consider variations of velocity with position.

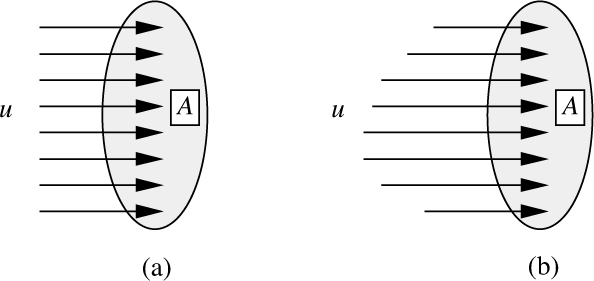
Velocity is not only important in its own right, but leads immediately to three fluxes or flow rates. Specifically, if u denotes a uniform velocity (not varying with position):

1. If the fluid passes through a plane of area A normal to the direction of the velocity, as shown in Fig. 1.6, the corresponding volumetric flow rate of fluid through the plane is Q = uA.

Fig. 1.6 Fluid passing through an area A: (a) Uniform velocity, (b) varying velocity.

2. The corresponding mass flow rate is m = ρQ = ρuA, where ρ is the (constant) fluid density. The alternative notation with an overdot, , is also used.

3. When velocity is multiplied by mass it gives momentum, a quantity of prime importance in fluid mechanics. The corresponding momentum flow rate passing through the area A is  = mu = ρu²A.

If u and/or ρ should vary with position, as in Fig. 1.6(b), the corresponding expressions will be seen later to involve integrals over the area A: 

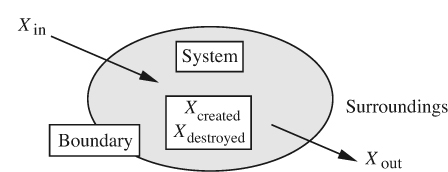
Basic laws. In principle, the laws of fluid mechanics can be stated simply, and—in the absence of relativistic effects—amount to conservation of mass, energy, and momentum. When applying these laws, the procedure is first to identify a system, its boundary, and its surroundings; and second, to identify how the system interacts with its surroundings. Refer to Fig. 1.7 and let the quantity X represent either mass, energy, or momentum. Also recognize that X may be added from the surroundings and transported into the system by an amount X_in across the boundary, and may likewise be removed or transported out of the system to the surroundings by an amount X_out.

Fig. 1.7 A system and transports to and from it.

The general conservation law gives the increase ΔX_system in the X-content of the system as:

Although this basic law may appear intuitively obvious, it applies only to a very restricted selection of properties X. For example, it is not generally true if X is another extensive property such as volume, and is quite meaningless if X is an intensive property such as pressure or temperature.

In certain cases, where Xⁱ is the mass of a definite chemical species i, we may also have an amount of creation  or destruction  due to chemical reaction, in which case the general law becomes:

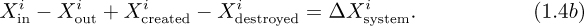
The conservation law will be discussed further in Section 2.1, and is of such fundamental importance that in various guises it will find numerous applications throughout all of this text.

To solve a physical problem, the following information concerning the fluid is also usually needed:

1. The physical properties of the fluid involved, as discussed in Section 1.4.

2. For situations involving fluid flow, a constitutive equation for the fluid, which relates the various stresses to the flow pattern.

1.4. Physical Properties—Density, Viscosity, and Surface Tension

There are three physical properties of fluids that are particularly important: density, viscosity, and surface tension. Each of these will be defined and viewed briefly in terms of molecular concepts, and their dimensions will be examined in terms of mass, length, and time (M, L, and T). The physical properties depend primarily on the particular fluid. For liquids, viscosity also depends strongly on the temperature; for gases, viscosity is approximately proportional to the square root of the absolute temperature. The density of gases depends almost directly on the absolute pressure; for most other cases, the effect of pressure on physical properties can be disregarded.

Typical processes often run almost isothermally, and in these cases the effect of temperature can be ignored. Except in certain special cases, such as the flow of a compressible gas (in which the density is not constant) or a liquid under a very high shear rate (in which viscous dissipation can cause significant internal heating), or situations involving exothermic or endothermic reactions, we shall ignore any variation of physical properties with pressure and temperature.

Densities of liquids. Density depends on the mass of an individual molecule and the number of such molecules that occupy a unit of volume. For liquids, density depends primarily on the particular liquid and, to a much smaller extent, on its temperature. Representative densities of liquids are given in Table 1.1.² (See Eqns. (1.9)–(1.11) for an explanation of the specific gravity and coefficient of thermal expansion columns.) The accuracy of the values given in Tables 1.1–1.6 is adequate for the calculations needed in this text. However, if highly accurate values are needed, particularly at extreme conditions, then specialized information should be sought elsewhere.