Design Equations for Flow Reactors

For a batch reactor, we saw that conversion increases with time spent in the reactor. For continuous-flow systems, this time usually increases with increasing reactor volume, e.g., the bigger/longer the reactor, the more time it will take the reactants to flow completely through the reactor and thus, the more time to react. Consequently, the conversion X is a function of reactor volume V. If F_A0 is the molar flow rate of species A fed to a system operated at steady state, the molar rate at which species A is reacting within the entire system will be F_A0X.

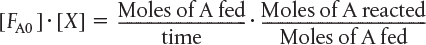
The molar feed rate of A to the system minus the rate of reaction of A within the system equals the molar flow rate of A leaving the system F_A. The preceding sentence can be expressed mathematically as

Rearranging gives

The entering molar flow rate of species A, F_A0 (mol/s), is just the product of the entering concentration, C_A0 (mol/dm³), and the entering volumetric flow rate, υ₀ (dm³/s).

Liquid phase

For liquid systems, the volumetric flow rate, υ, is constant and equal to υ₀, and C_A0 is commonly given in terms of molarity, for example, C_A0 = 2 mol/dm³.

For gas systems, C_A0 can be calculated from the entering mole fraction, y_A0, the temperature, T₀, and pressure, P₀, using the ideal gas law or some other gas law. For an ideal gas (see Appendix B):

Gas phase

Now that we have a relationship [Equation (2-8)] between the molar flow rate and conversion, it is possible to express the design equations (i.e., mole balances) in terms of conversion for the flow reactors examined in Chapter 1.

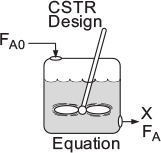
2.3.1 CSTR (Also Known as a Backmix Reactor or a Vat)

Recall that the CSTR is modeled as being well mixed such that there are no spatial variations in the reactor. For the general reaction

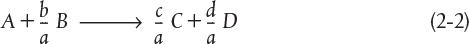
the CSTR mole balance Equation (1-7) can be arranged to

We now substitute for F_A in terms of F_A0 and X

and then substitute Equation (2-12) into (2-11)

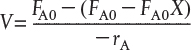
Simplifying, we see that the CSTR volume necessary to achieve a specified conversion X is

Perfect mixing

Because the reactor is perfectly mixed, the exit composition from the reactor is identical to the composition inside the reactor, and, therefore, the rate of reaction, −r_A, is evaluated at the exit conditions.