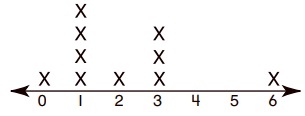Category: Mean Median and Mode

Introduction

We can find either of the three measures of center for a given data set. However, we find that one of the three is the best measure to describe the given data.

Rules to find the best measure to describe data

• If the data points do not repeat and if there are no extreme values the best measure of center to describe a data set is mean.
• If some of the data points repeat, the one that has maximum occurrence is the mode, which is the best measure of center in this case for the data set.
• If the data set has some extremely low or extremely high values as compared to other numbers in the data set, the best measure of center for the data set is the median.

Example 1

Which is the best measure to describe set of data given below?

17, 12, 18, 10, 15, 11, 12, 16, 19

Solution

Step 1:

There are no repeating data and no extreme values.

Step 2:

So the best measure to describe given data is Mean.

Example 2

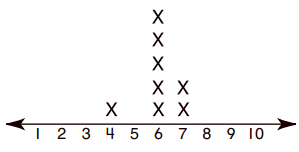
25 , 29 , 36 , 35 , 36 , 26 , 24 , 37 , 22 , 28 , 36

Solution

Step 1:

Some of the data repeat for example 36

Step 2:

So the best measure to describe given data is Mode.

Introduction

Outliers are data points that dont fit the pattern of rest of the numbers. They are the extremely high or extremely low values in the data set.

A simple way to find an outlier is to examine the numbers in the data set. We will see that most numbers are clustered around a range and some numbers are way too low or too high compared to rest of the numbers. Such numbers are known as outliers.

Other definition of an outlier

A data point that is distinctly separate from the rest of the data. One definition of outlier is any data point more than 1.5 interquartile ranges IQRs below the first quartile or above the third quartile. The interquartile range IQR is the difference between the third quartile and the first quartile of the data set.

Example 1

Find the outliers for the data 0, 2, 5, 6, 9, 12, 35.

Solution

For given data set, we have the following five-number summary.

minimum = 0

first quartile = 2

median = 6

third quartile = 12

maximum = 35

IQR = 12 2 = 10, so 1.5IQR = 15.

To determine if there are outliers we must consider the numbers that are 1.5IQR or 15 beyond the quartiles.

first quartile 1.5IQR = 2 15 = 13

third quartile + 1.5IQR = 12 + 15 = 27

Since 35 is outside the interval from 13 to 27, 35 is the outlier in this data set.

Example 2

Find the outliers in the given data set below.

28, 26, 29, 30, 81, 32, 37

Solution

Step 1:

The data that is different from other numbers in the given set is 81

Step 2:

So the outlier for this data set is 81

Example 3

Introduction

In this lesson we are given a data set. We find its mean and median. Then one of its data is changed. We then find the changed mean and changed median after one of the data has been changed.

Example 1

Find new mean and new median of the data set if a data is changed.

12, 15, 18, 13, 6, 14; 13 is changed to 5

Solution

Step 1:

Mean = (12+15+18+13+6+14)6 = 13; Median = 13.5

Step 2:

With data change

New Mean = (12+15+18+5+6+14)6 = 11.67; New Median = 13

Example 2

Find new mean and new median of the data set if a data is changed.

18, 15, 11, 3, 8, 4, 13, 12, 3; 15 is changed to 18

Solution

Step 1:

Mean = (18+15+11+3+8+4+13+12+3)9 = 9.67; Median = 11

Step 2:

With data change

New Mean = (18+18+11+3+8+4+13+12+3)9 = 10 ; New Median = 11

Introduction

The median of data set is found as follows. The numbers of the data set are arranged in an increasing ordecreasing order. We look for the middle number in the data set and it is the median of the data set. If the number data are odd, there will be one middle number which will be the median. If the number of data are even, there will be two middle numbers and the average of these numbers gives the median of the data set.

Example 1

Find the mean and median of the following data set.

70, 68, 56, 62, 56, 66, 56

Solution

Step 1:

Mean of the data = (70+68+56+62+56+66+56)7 = 62

Step 2:

Data set in increasing order − 56, 56, 56, 62, 66, 68, 70.

Middle score is 62

Median of data set = 62

Example 2

Find the mean and median of the given data set.

94, 79, 81, 79, 87

Solution

Step 1:

Mean of the data = (94+79+81+79+87)5 = 84

Step 2:

Data set in increasing order − 79, 79, 81, 87, 94

Middle score is 81

Median of data set = 81

Introduction

In this lesson, we are given a data set. We are given a new mean of the data set and are required find a new data member which when added will yield the new mean of the changed data set.

Rules to find new score that will yield a new given mean

• We start by taking the new score as x.
• We add x to the sum of data to find the new sum of data.
• If the number of data were n, now we have n+1 as the new number of data.
• Equating new sum of data divided by n+1 to the new mean and solving we find the value of new score x.

Example 1

Find the value for a new score that will yield a given mean.

8, 12, 8, 10, 18, 12, 4; New mean = 11

Solution

Step 1:

Let the new score to be added = x

Step 2:

New mean = (8+12+8+10+18+12+4+x)8 = 11

= 72 + x = 88; x = 88 72 = 16

Step 3:

Required new score = 16.

Example 2

Find the value for a new score that will yield a given mean.

25, 18, 18, 13, 4, 17, 18, 19, 3; New mean = 17

Solution

Step 1:

Let the new score to be added = x

Step 2:

New mean = (25+18+18+13+4+17+18+19+3+x)10 = 17

= 135 + x = 170; x = 170 135 = 35

Step 3:

Required new score = 35

Introduction

In this lesson, we solve problems involving, the sample size, sum of a data set and its mean. Any two of these three quantities are given and we find the third unknown quantity using the relation between these 3 quantities.

Formula

• Mean=SumofthedataNumberofdata
• Sum of the data = Mean Number of data
• Numberofdata=SumofthedataMean

Example 1

The average of x and 3 is equal to the average of x, 6 and 9. Find x

1, 1, 4, 4, 5, 6, 7, 7, 10, 10

Solution

Step 1:

Average of x and 3 = (x+3)2

Average of x, 6, and 9 = (x+6+9)3

Step 2:

Given (x+3)2=(x+15)3

Solving we get 3x + 9 = 2x + 30 or

3x 2x = x = 30 9 = 21

Step 3:

So x = 21

Example 2

7 consecutive even integers have an average of 48. Find the average of the greatest two of those integers.

Solution

Step 1:

Let the consecutive even integers be

x 6, x 4, x 2, x, x + 2, x + 4, x + 6

Their average = (x6+x4+x2+x+x+2+x+4+x+6)7=7×7 = 48. So X=48

Step 2:

So the numbers are 42, 44, 46, 48, 50, 52, 54

The average of the two greatest of these integers 52 and 54 is 52+54/2 = 53

Introduction

Symmetrical distribution is a situation in which the values of variables occur at regular frequencies, and the mean, median and mode occur at the same point. Unlike asymmetrical distribution, symmetrical distribution does not skew.

Example 1

Find the mean of the following symmetric distribution.

1, 1, 4, 4, 5, 6, 7, 7, 10, 10

Solution

Step 1:

Mean of distribution = (1+1+4+4+5+6+7+7+10+10)10=5510 = 5.5

Step 2:

Or mean of middle two numbers = (5+6)2 = 5.5

So mean of symmetric distribution = 5.5

Example 2

Find the mean of the following symmetric distribution.

2, 2, 4, 4, 5, 6, 7, 7, 9, 9

Solution

Step 1:

Mean of distribution = (2+2+4+4+5+6+7+7+9+9)10=5510 = 5.5

Step 2:

Or mean of middle two numbers = (5+6)2 = 5.5

So mean of symmetric distribution = 5.5

Introduction

In this lesson we understand the mean of a dataset using graphical method.

Suppose we are given a bar graph showing two bars of data. Here we are required to find the mean of given data graphically.

Rules to find the mean graphically

• In the bar graph we find the heights of the two bars.
• The average or mean of these heights is found.
• We then draw a third bar with the average height found in second step.
• The height of this third bar gives the mean or average of given data set graphically.

Example 1

The two bars in a bar graph have heights 16 and 22. What height a new bar should have so that it has the mean height of the two bars?

Solution

Step 1:

Heights of given bars 16, 22

Step 2:

Mean height = (16+22)2=382 = 19

So height of new bar = 19

Example 2

The two bars in a bar graph have heights 15 and 27. What height a new bar should have so that it has the mean height of the two bars?

Solution

Step 1:

Heights of given bars 15, 27

Step 2:

Mean height = (15+27)2=422 = 21

So height of new bar = 21

Introduction

A line plot of a data set shows the various numbers of the data set along the x axis as per a convenient scale. It also shows the number of occurrences of each of the numbers as crosses. The smallest and largest numbers among the data set also find a place on the line plot.

By examining the line plot, we find the number with the maximum number of crosses or occurrences. This gives the mode of the data set.

We find the smallest and the largest number from the data set and find their difference and this difference is the range of the given data set.

This is how the mode and range of a data set is found from its line plot.

Example 1

Find the mode and range from the following line plot

Solution

Step 1:

The number that repeats most is 1; Mode = 1

Step 2:

Range = Max number Min number

= 6 0 = 6

Step 3:

Mode = 1; Range = 6

Example 2

Find the mode and range from the following line plot −

Solution

Step 1:

The number that repeats most is 6; Mode = 6

Step 2:

Range = Max number Min number

= 7 4 = 3

Step 3:

Mode = 6; Range = 3

Introduction

Range is a measure of variance of the data. The measure of centre gives an average value of the data set while the range gives a measure of how far the data is spread out.

Rules to find the range of a data set

• We look at the numbers of the data set and find the smallest and the largest numbers among them.
• The difference between the largest number and the smallest number gives the range of the data.

Example 1

Find the mode and range of the set of numbers given below −

14, 29, 14, 36, 78

Solution

Step 1:

The number that repeats most is 14; So Mode = 14.

Step 2:

Range = greatest number smallest number

= 78 14 = 64.

Step 3:

Mode = 14; Range = 64.

Example 2

Find the mode and range of the set of numbers given below −

22, 59, 53, 85, 53, 34, 17

Solution

Step 1:

The number that repeats most is 53; So Mode = 53.

Step 2:

Range = greatest number smallest number

= 85 17 = 68.

Step 3:

Mode = 53; Range = 68.