Models for Shear Stress

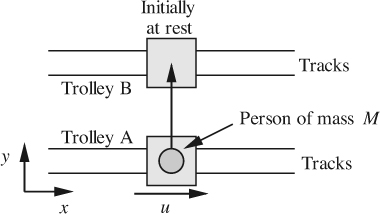
Newton’s law of viscosity relating the shear stress to the velocity gradient has a ready interpretation based on momentum transport resulting from molecular diffusion. As an introduction, consider first the situation in Fig. 3.7, which shows a plan of two trolleys on frictionless tracks.

Fig. 3.7 Lateral transport of momentum between two trolleys on frictionless tracks.

A person of mass M jumps from trolley A, which is moving to the right with velocity u, onto trolley B, which is hitherto stationary. The person clearly transports an amount of momentum M = Mu from A to B, with the result that B accelerates; note that the momentum is in the x direction, but that it is transported in the transverse or y direction. If the transfer were continuous, with several people jumping successively—assuming that the trolley is large enough to accommodate them—the net effect would be a steady force in the x direction exerted by A on B, analogous to a shear force.

Momentum transport in laminar flow. A similar phenomenon occurs for laminar flow, except that the lateral transport is now due to random molecular movement, known as Brownian motion.³

³ G. Stix, Scientific American, Vol. 291, No. 3, September 2004, p. 46, says: “[In 1905] Albert Einstein published a paper in Annalen, ‘On the motion of small particles suspended in liquids at rest required by the molecular-kinetic theory of heat,’ that supplied a prediction of the number and mass of molecules in a given volume of liquid—and how these molecules would flit around. The erratic movements were known as Brownian motion, after the observation by botanist Robert Brown in 1827 of the irregular zigs and zags of particles inside pollen grains in water. Einstein suggested that the movements of the water molecules would be so great that they would jostle suspended particles, a dance that could be witnessed under a microscope.”

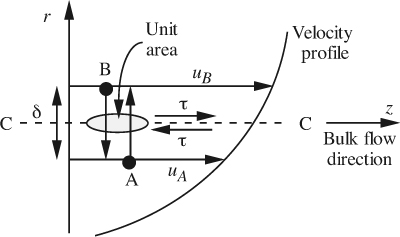
Fig. 3.8 shows part of the velocity profile for flow in the axial or z direction of a pipe. Consider a plane C–C at any radial location. Because of Brownian motion, molecules such as those at A and B will constantly be crossing C–C from below and above, at a mass rate m per unit area per unit time. A molecule such as B, whose z component of velocity is u_B, will bring down with it a slightly larger amount of z momentum than that taken upward by a molecule such as A, whose z component of velocity is only u_A. For a velocity profile as shown, there is a net positive rate of transfer of z momentum downward across C–C, and this is manifest as a shear stress given by:

Fig. 3.8 Molecular diffusion model for shear stress in laminar flow.

On the average, the molecules will travel a small distance δ, known as their mean free path, before they collide with other molecules and surrender their momentum. The velocity discrepancy u_B – u_A is therefore the product of δ and the local velocity gradient, yielding Newton’s law of viscosity:

where μ = mδ is the viscosity of the fluid. Since both m and δ are independent of the flow rate in the z direction, the viscosity is constant, independent of the bulk motion. Note that we now have a physical basis for the similar result of (3.4), in which the minus sign merely reflects an alternative viewpoint for the direction of the shear stress.

Newton, Sir Isaac, born 1642 in Lincolnshire, England; died 1727 in Kensington, buried in Westminster Abbey, London. He was an unsur-passed scientific genius. After a brief interruption of his education to help with the family farm, he entered Trinity College Cambridge as a student in 1661, obtained his B.A. degree in mathematics in 1665, and was elected a fellow of his college in 1667. Newton’s research in optics embraced reflection, refraction, and polarization of light, and he invented a reflecting telescope. About 1666, he deduced from Kepler’s laws of planetary motion that the gravitational attraction between the sun and a planet must vary inversely as the square of the distance between them. Newton was appointed Lucasian professor of mathematics in 1669, and elected a fellow of the Royal Society in 1671. His magnum opus was Philosophiæ Naturalis Principia Mathematica; published in three volumes in 1687, “Principia” included the laws of mechanics, celestial motions, hydrodynamics, wave motion, and tides. At this stage, despite all of his accomplishments, Newton had neither been rewarded monetarily nor with a position of national prominence. However, matters improved when he was appointed Master of the Royal Mint in London in 1699, a position he held with distinction until his death.

Source: The Encyclopædia Britannica, 11th ed., Cambridge University Press (1910–1911).

For gases, the mean free path can be predicted from kinetic theory, leading to the following theoretical expression for the viscosity, which is found to agree well in most cases with experiment, provided the pressure is less than approximately 10 atm:

Here, r is the effective radius of a gas molecule and m is its mass; k is Boltzmann’s constant (1.380 × 10 ^–16 ergs/molecule K) and T is the absolute temperature. Note the predictions that: (a) μ is independent of pressure, and (b) μ rises with increasing temperature.

For liquids, there is no simple corresponding expression for their viscosities. In general, however—and in contrast to gases—the viscosity of liquids falls with increasing temperature. Note also the empirical correlations of Eqns. (1.17) and (1.18) for the viscosities of liquids and gases, which are based on experimental observations.

Momentum transport in turbulent flow. An analogous situation holds for turbulent flow. However, the random molecular motion is now substantially augmented by a turbulent eddy motion, which is on a much larger scale. Turbulent flow can be described by the concept of the eddy kinematic viscosity, ν_T, giving:

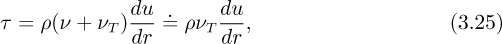
it being noted—from experiment—that ν_T ≫ ν. The eddy kinematic viscosity ν_T is not constant, but is found experimentally to be approximately directly proportional to u_mD, where D is the pipe diameter; this result is also plausible on qualitative grounds—an increase in u_m causes more turbulence and a larger D permits eddies to travel further. The momentum transport is also proportional to the fluid density. Since du/dr is also roughly proportional to u_m (a doubling of u_m also approximately doubles the velocity gradient at any position), and inversely proportional to D, it follows that:

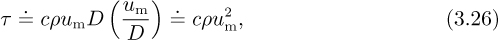
in which c is a constant, as yet unknown, and which depends on the particular radial location we are examining. A more detailed discussion of the eddy viscosity